Séminaire Interfaces des mathématiques et systèmes complexes

Séminaires à Venir

 

---------------------------------------------------------------------------------------------

 

Archives

 

Archives vidéos (2009-2011) [1]

 

Archives séminaires (2011-2019) [2]

 

Vendredi  8  Novembre 2019  à 11 h (salle de conf du LJAD)

Oleksandr Chepizhko (Innsbruck Univ.)

'Transport properties of circle microswimmers in heterogeneous media '

Abstract:

We simulate the dynamics of a single circle microswimmer exploring a disordered array of fixed obstacles. The microswimmer moves on circular orbits in the freely accessible space and follows the surface of an obstacle for a certain time upon collision. Two cases are considered, an ideal microswimmer[1] and a microswimmer subject to rotational diffusion[2]. Depending on the obstacle density and the radius of the circular orbits, the microswimmer displays either long-range transport or is localized in a finite region.
We show that for the ideal microswimmer there are transitions from two localized states to a diffusive state each driven by an underlying static percolation transition. We determine the non-equilibrium state diagram and calculate the mean-square displacements and diffusivities by computer simulations. Close to the transition lines transport becomes subdiffusive which is rationalized as a dynamic critical phenomenon.
The interplay of two different types of randomnesses, quenched disorder and time-dependent noise, is investigated to unravel their impact on the transport properties of the microswimmer subject to the rotational diffusion. We compute lines of isodiffusivity as a function of the rotational diffusion coefficient and the obstacle density. We find that increasing noise or disorder tends to amplify diffusion, yet for large randomness the competition leads to a strong suppression of transport. We rationalize the suppression and amplification of transport by comparing the relevant time scales of the free motion to the mean-free path time between collisions with obstacles.

1. O. Chepizhko, T. Franosch, Soft Matter, 2019, 15, 452
2. O. Chepizhko, T. Franosch, submitted

 

Mardi 17 Décembre 2019 à 14 heures en salle Fizeau du LJAD

Prof. Aziz-Aloui (Université du Havre) LMAH, ISCN, FR-CNRS-3335, France.

" Systèmes complexes et réseaux d'interaction. Application au comportement
asymptotique de réseaux de systèmes de réaction-diffusion en neuroscience et en écosystèmes "

"Complex Systems and Interaction Networks: Application to the Asymptotic
Behavior of Networks of Reaction-Diffusion Systems in Neuroscience
and Ecosystems"

Abstract:

Neuroscience consists of the study of the nervous system and especially the brain.
The neuron is an electrically excitable cell processing and
transmitting information by electrical and chemical signaling, the
latter via synapses, specialized connections with other cells.
A. L. Hodgkin and A. Huxley proposed the first neuron
model to explain the ionic mechanisms underlying the initiation and
propagation of action potentials in the squid giant axon. Here, we
are interested in the asymptotic behavior of complex networks of
reaction-diffusion (PDE) systems of such neuron models. We show the
existence of the global attractor and the identical synchronization
for the network. We determine analytically, for a given network
topology, the onset of such a synchronization. We then present
numerical simulations and heuristic laws giving the minimum coupling
strength necessary to obtain the synchronization, with respect to the
number of nodes and the network topology.

 

Vendredi 17 Février 2023 à 11 heures en salle de conférence du LJAD

(séminaire joint IMSC-EDPAN)

Dr. Eugenio Pozzoli (Dipartimento di Matematica "Tullio Levi-Civita",
Università degli studi di Padova), Italie.

" Small-time control of strongly driven quantum rotors"

Abstract:

We consider a strongly driven quantum rotor, modelled as a Schrödinger
PDE (on the two-dimensional sphere) forced via low modes multiplicative
controls. This system is used in quantum chemistry and quantum
information processing. We present a geometric control strategy for
inducing transitions between particular rotational eigenstates in
arbitrarily small time. Roughly speaking, the first step consists in
sending two impulsions with opposite sign, with a very short time delay.
These opposite kicks permit to recover directions (a.k.a. Lie brackets)
that are not directly accessible.

 

 

Lundi 6 Mars 2023 à 14 heures en salle de conférence du LJAD

(séminaire joint IMSC-Axe Math-Bio)

Dr. Rachele Allena (LJAD).

video here [3]

"Mathematical and mechanical modelling of cell migration"

Abstract:

Cell migration plays a fundamental role in several processes such as bone remodelling, cancer, embryogenesis and immune response.
During the last decades, biologists have started exploring the role of mechanics and more specifically of forces, stresses and strains exerted and undergone by the cells during their movement. Although
important advances have been made in imaging in vitro migration,
mathematical modelling remains a very useful and powerful tool to
explore a large number of scenarios and to quantify specific parameters
of such a complex mechanobiological phenomenon.

I will present a series of mathematical models allowing to simulate cell migration in different configurations
including migration over homogeneous and heterogenous substrates, under
confinement, in presence of durotaxis or in a collective manner.
The comparison of the numerical results with the experimental
observations prove the consistency of the mechanical and mathematical
approach and makes it possible to consider the setting up of mechanotherapies.

 

Jeudi 16 Mars 2023 à 14 heures en salle Fizeau du LJAD

(séminaire joint IMSC - PS - Axe Math-Bio)

Dr. Guilherme Ost   (Institute of Mathematics of the Federal University of Rio de Janeiro)  

"Stochastic modeling of biological neural networks and animal behavior"

Abstract:

A central question in neuroscience is to understand how large-scale brain dynamics emerge from the interactions between individual neurons. A popular approach for addressing this question is to consider large-scale limits of interacting point processes modeling the neural activity, assuming that the interaction between the components of the model is of mean-field type (“uniform”). However, as I will show in the talk, in such mean-field limits the evolution of any pair of components (the neurons) become independent, contrarily to what is often observed in empirical data. This leads naturally to the following question: if neurons do not interact in a mean-field way, how do they interact? A crucial step to answer this question is to design methods to reconstruct the potential interactions between neurons from their spiking activity. Here I will briefly show some statistical methods to neural interaction reconstruction that I have proposed with some collaborators, discussing also some of their limitations. After that, in the remaining part of my talk,I will present a random walk model that modifies the dynamics depending on its trajectory, motivated by the following question: why did we observe just a few behavioral states in animals, although they typically have a large degree of freedom for producing movements?The standard approach for the predominance of a subset of behavior in an individual is to assume a learning mechanism. Here, I will show that it is also possible to observe only a few dominant behaviors, despite the lack of learning.

 

Lundi 27 Mars 2023 à 14 heures en salle Fizeau du LJAD

(séminaire joint IMSC - Axe Math-Bio)

Léo Meyer (Université d'Orléans)

"Modeling adipose cell distribution using Lifshitz-Slyozov and Becker-Döring equations"

Adipose cells or adipocytes are the specialised cells composing the adipose tissue in a variety of species.
Their role is the storage of energy in the form of a lipid droplet inside their membrane. Based on the
amount of lipid they contain, one can consider the distribution of adipocyte per amount of lipid and
observe a peculiar feature : the resulting distribution is bimodal, thus having two local maxima. The
aim of this talk is to introduce a model built from the work in [1] that is able to reproduce this bimodal
feature.
Considering that cells are spheres and that our system is closed (no loss of lipids) the following set of
equation can be derived :

∂ t f (t, x) + ∂ x (v(x, L(t))f (t, x)) = 0, (t, x) ∈ R 2+

L(t) + R + xf (t, x)dx = λ, t ∈ R +
Where f : (t, x) ∈ R 2+ → R + is the distribution of adipocyte per amount of lipid x and L : t ∈ R + → R + is

the amount of lipids available in the medium. The transport speed v(x, L) takes the form
a(x)M (L) − b(x), where a is the lipid inflow rate and b the lipid outflow rate. The function M represents
the dependency of the inflow rate to the outside resource, i.e. the lipids in the medium. The value λ is
the total amount of lipids in the system and is assumed to be constant in time.
This coupling of a transport equation and a conservation equation of this form is related to the
Lifshitz-Slyozov model introduced in [2]. We will introduce a related set of equations for the adipose
cells : the Becker-Döring equations [3] and prove the classical result of convergence from one to another.
We will also present some extensions to the model using a transport-diffusion equation arising from the
previous convergence result and a rewriting of the model using stochastic processes. In both cases, we
shall describe stationary solutions. Finally, we will present some numerical results using a standard finite
volume scheme introduced in [4] for the transport and transport-diffusion models.
References [1] Soula, H. A., et al. ”Modelling adipocytes size distribution.” Journal of theoretical biology 332
(2013): 89-95.
[2] Lifshitz, Ilya M., and Vitaly V. Slyozov. ”The kinetics of precipitation from supersaturated solid
solutions.” Journal of physics and chemistry of solids 19.1-2 (1961): 35-50.
[3] Becker, Richard, and Werner Döring. ”Kinetische behandlung der keimbildung in übersättigten
dämpfen.” Annalen der physik 416.8 (1935): 719-752.
[4] Goudon, Thierry, and Laurent Monasse. ”Fokker–Planck Approach of Ostwald Ripening: Sim-
ulation of a Modified Lifshitz–Slyozov–Wagner System with a Diffusive Correction.” SIAM Journal on
Scientific Computing 42.1 (2020): B157-B184.

 

Mardi 6 Juin 2023 à 11 heures en salle Fizeau du LJAD

(séminaire joint IMSC - Axe Math-Bio)

Florence Hubert (Aix-Marseille Université)

 

"Growth fragmentation models in oncology"

Growth fragmentations models are often used in structured
population dynamics to model for example cell division,
polymerization. The classical form of the equation is

 

 

 

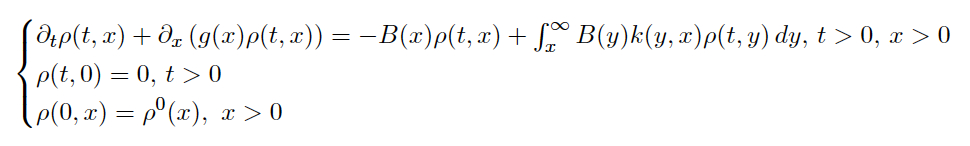
The wellposeness of a solution globally defined to this equation
as well as its asympototic behaviour has been widely studied. We
will first give some contexts where this model is used. We will
then recall the main results (see [1], [4]). We will also propose
extensions of such equation in the context of metastasis spreading
and in the context of microtubule dynamical instabilities. We will
make a point on the properties of these models and the remaining
challenges.

 

References
[1] J. A. Cañizo, P. Gabriel, and H. Yoldas. Spectral gap for the
growthfragmentation equation via Harris’s theorem. SIAM J. Math.
Anal., Vol.53, No.5, pp.5185-5214,(2021)
[2] N. Hartung, S. Mollard, D. Barbolosi, A. Benabdallah, G.
Chapuisat, G. Henry,S. Giacometti, A. Iliadis, J.Ciccolini, C.
Faivre, F. Hubert. Mathematical Modeling of tumor growth and
metastatics spreading : validation in tumor-bearing mice, Cancer
Research 74, p. 6397-6407, 2014.
[3] S. Honoré, F. Hubert, M. Tournus, D. White. A
growth-fragmentation approach for modeling microtubule dynamic
instability, Bulletin of Mathematical Biology, 81 p. 722–758
(2019)
[4] B. Perthame. Transport equations in biology, Springer.

 

 

Vendredi 16 Juin 2023 à 11 heures en salle Fizeau du LJAD

(séminaire joint IMSC - Axe Math-Bio)

Frédéric Paquin-Lefebvre (Sorbonne Université)

"Problèmes d'échappée belle dans les microdomaines organisés
en réseaux."

La dynamique intracellulaire des molécules et ions à la
recherche d'une cible est souvent modélisée par un processus
de diffusion. Chaque particule, qu'on suppose Brownienne, suit
une trajectoire stochastique à l'intérieur d'un domaine
confiné correspondant à un compartiment cellulaire. Toute la
frontière du domaine est réfléchissante à l'exception de
quelques fenêtres étroites, d'où les particules Browniennes
peuvent s'échapper. Le calcul du temps de sortie moyen, aussi
désigné problème d'échappée belle, nécessite la résolution
d'une équation de Poisson avec conditions aux bords de type
mixte Dirichlet-Neumann. Lors de cet exposé je vais présenter
quelques exemples de problèmes d'échappée belle dans des
microdomaines cellulaires modélisés par des réseaux 3-D de
sphères reliés par des tubes cylindriques étroits. L'objectif
sera de mettre en valeur l'influence des paramètres
géométriques sur les temps de sortie, et ultimement sur les
échelles de temps des réactions biochimiques intracellulaires.