


suivant: Énergie cinétique
monter: Équations du modèle
précédent: Développements par rapport à
Table des matières
Nous allons maintenant discuter du choix des conditions aux bords du
système (4.25). Soit
 la
frontière du bassin. Nous imposerons sur la vitesse horizontale
la
frontière du bassin. Nous imposerons sur la vitesse horizontale
 une condition de glissement à la paroi :
une condition de glissement à la paroi :
 |
(4.27) |
où  est la normale extérieure au domaine. Si
est la normale extérieure au domaine. Si  est la
tangente à la frontière, la condition précédente traduite en
terme de fonction de courant devient
est la
tangente à la frontière, la condition précédente traduite en
terme de fonction de courant devient
 sur
sur  . On en déduit donc que
. On en déduit donc que
 est constant sur
est constant sur  . La frontière coïncide donc
avec une ligne de courant. De plus,
. La frontière coïncide donc
avec une ligne de courant. De plus,  étant défini à une
constante près, on peut imposer sur le bord
étant défini à une
constante près, on peut imposer sur le bord  .
.
En reprenant la condition au bord (4.27), on a
 . En développant
cette dernière équation, on obtient :
. En développant
cette dernière équation, on obtient :
en appelant 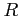 le rayon de courbure de la frontière au point
considéré. Pour un domaine carré ou rectangulaire,
le rayon de courbure de la frontière au point
considéré. Pour un domaine carré ou rectangulaire, 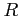 est
infini, donc son inverse est nul, et choisir
est
infini, donc son inverse est nul, et choisir  le long de
le long de
 revient à considérer que la vitesse de l'écoulement le
long des frontières n'est pas perturbée normalement à
celles-ci. C'est la condition que l'on s'impose.
revient à considérer que la vitesse de l'écoulement le
long des frontières n'est pas perturbée normalement à
celles-ci. C'est la condition que l'on s'impose.
Les conditions aux bords choisies sont donc :
 |
(4.28) |



suivant: Énergie cinétique
monter: Équations du modèle
précédent: Développements par rapport à
Table des matières
Retour à la page principale
![]() la
frontière du bassin. Nous imposerons sur la vitesse horizontale
la
frontière du bassin. Nous imposerons sur la vitesse horizontale
![]() une condition de glissement à la paroi :
une condition de glissement à la paroi :
 sur
sur  . En développant
cette dernière équation, on obtient :
. En développant
cette dernière équation, on obtient :
