Bifurcations vers des tores invariants pour les mappings [20, 21, 33]   Le but était de comprendre notamment certains résultats expérimentaux sur la convection de Bénard-Rayleigh en petite boîte, où plusieurs fréquences apparaissent après une succession de bifurcations. Dans les deux premiers articles [20] (90p.), [21] (1979) avec A. Chenciner (Paris), nous donnons des conditions suffisantes sur une famille de mappings ayant un tore invariant, afin d'obtenir une bifurcation vers un tore de dimension plus grande. Ces conditions portent sur l'opérateur linéarisé, incluant des conditions diophantiennes sur le nombre de rotation et sur les valeurs propres, semblant très restrictives à cette époque. Cependant, quelques années plus tard, nous avons montré, avec J.Los [33] (1988) (Marseille) que ces bifurcations peuvent apparaître quasi-génériquement, au sens qu'un paramètre additionnel donne une description de telles bifurcations sur un ensemble de Cantor de l'espace des paramètres.

          Bifurcation vers des patterns quasi-périodiques [82] (2009) Avec A.Rucklidge (Leeds), nous  étudions les patterns spatialement quasi-périodiques, comme dans l'expérience de Faraday (où on secoue périodiquement une couche de fluide horizontale), et dans la convection de Bénard-Rayleigh. On utilise des estimations Gevrey pour prouver l'existence de solutions quasi-périodiques de l'équation aux dérivées partielles modèle de Swift-Hohenberg (dans le plan), à un reste exponentiellement petit près. Dans [C35] (2009) je montre que ce résultat s'étend au problème de convection stationnaire de Bénard-Rayleigh. Dans [86] avec M.Argentina (Nice) nous considérons le "vrai" problème de Faraday dans une couche mince de fluide visqueux soumise à une oscillation harmonique verticale. Nous donnons un nouveau processus pour obtenir formellement un quasipattern en partant d'une instabilité où les oscillations à la fréquence moitié et celles à la fréquence de forçage sont critiques en même temps. Dans [89] avec B.Braksmaa et L.Stolovitch, nous donnons la première preuve mathématique (difficulté liée à la présence de "petits diviseurs") de  la bifurcation de quasipatterns pour l'EDP de Swift-Hohenberg. Dans [92] on montre que la superposition de deux  patterns  périodiques hexagonaux, donne en général un quasipattern de structure dodécagonale, voir des résultats généraux dans l'article  [94] avec A.Rucklidge (figure ci-dessous).  Dans [90]  , avec B.Braaksma, on montre que les résultats d'existence s'étendent à la convection de Bénard-Rayleigh (long et technique).

 

Le problème de Couette-Taylor  [27, 28, 38, 42, 44], Livre: [M3] 

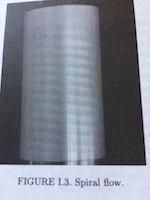
Ces articles et le livre [M3] (1994) écrit avec P.Chossat, étudient le problème de Couette-Taylor (problème vieux de plus d'un siècle) des instabilités d'un fluide visqueux compris entre deux cylindres co-axiaux en rotations uniformes. Ma petite équipe et moi-même avons travaillé environ 10 ans, théoriquement et numériquement, sur ce sujet, en concertation avec des équipes expérimentales américaines (H.Swinney, R.Tagg, D.Andereck) permettant des découvertes, des comparaisons et des confirmations, y compris quantitatives . Nous avons pu prédire (1985) par exemple la structure en "rubans" qu'on peut obtenir lorsque l'écoulement de Couette perd sa stabilité alors que les cylindres tournent en sens contraires. Cet écoulement a été observé plus tard par R.Tagg (Colorado) et correspond à des ondes stationnaires dans la direction axiale, et rotatives dans la direction azimuthale. Nous avons en fait utilisé de façon systématique la réduction à une variété centrale et les symétries brisées par les modes critiques, afin d'aboutir (en les justifiant) à des équations d'amplitudes faciles à étudier. De plus, [27] (1986) donne une preuve simple d'une telle réduction au voisinage d'une orbite de groupe non triviale (cercle, tore,...), et permet d'expliquer simplement la grande variété des écoulements physiquement observés, qui bifurquent quand les rouleaux de Taylor perdent leur stabilité.  Dans [28] (1987) nous étudions la compétition entre deux types de modes critiques oscillants, qui se réduit à l'étude d'un système différentiel de dimension 8 (variété centrale), et permet d'interpréter quelques résultats expérimentaux de l'équipe d'Andereck (Ohio) et R.Tagg (Colorado), comme le régime en "spirales interpénétrantes". Dans [38] (1989) et [44] (1991) avec A.Mielke (Stuttgart), nous étudions les solutions stationnaires ou périodiques du temps, en ne faisant plus l'hypothèse de périodicité axiale. Ici la coordonnée axiale joue le rôle du temps dans un système qui est alors réversible. Ceci donne de nouvelles solutions des équations de Navier-Stokes, comme des solutions axialement quasi-périodiques ([42] avec J.Los, 1990), des solutions ressemblant à l'écoulement de Couette au centre, et aux rouleaux de Taylor aux extrémités, et nous montrons aussi l'existence d'une solution de type "défaut" connectant deux écoulements en ondes hélicoïdales symétriques. Cet écoulement est souvent observé en premier pour une certaine plage des paramètres où les cylindres tournent en sens inverses.
Le livre [M3] constitue la réponse à la plupart des questions posées par R.Feynman sur le problème de Couette-Taylor ("one of the most challenging problems in fluid mechanics") à la fin du second volume sur l'électromagnétisme, de son fameux cours de physique.

Formes Normales générales et applications

La section sur le problème de Couette-Taylor utilise déjà la réduction à une forme normale pour arriver à des équations aux amplitudes (variété centrale) faciles à étudier, grâce aux symétries du système. Cette réduction est également utilisée en théorie des vagues (voir le chapitre suivant) dans le cadre des systèmes réversibles. Cette section concerne les résultats généraux et d'autres applications que celles citées ci-dessus. 

Les formes normales et les systèmes réversibles , [29, 31, 40], [69], [74], Livres: [M4], [M5], [M6]

La recherche de "formes normales pour simplifier l'étude locale de champs de vecteurs au voisinage d'une situation singulière, est un sujet qui remonte à Poincaré, Birkhoff et, plus récemment, V.Arnold. L'article [29] (1987) qui est mon article le plus cité, résulte d'une collaboration notamment avec des physiciens chiliens, et permet une caractérisation simple des formes normales, utilisant seulement des outils analytiques élémentaires (évitant la géométrie algébrique). Une partie de notre résultat est en fait inclus dans un article antérieur (peu lisible) de Belitskii. Notre résultat est maintenant classique est fait  partie de logiciels de calculs (livre de S.N.Chow). L'article [31] (1988) étend le résultat aux champs de vecteurs périodiques du temps. Dans [40] (1990, mon 2ème article le plus cité) avec P.Coullet, nous donnons la liste des 10 bifurcations génériques possibles d'un pattern stationnaire périodique dans une direction, solution d'un système invariant par translation et réflection (comme dans de nombreux problèmes d'instabilités hydrodynamiques). Nous donnons notamment la preuve qu’une bifurcation avec rupture de la symétrie de réflection pour un pattern périodique d'un tel système, peut produire une onde progressive lente. Cet article reste une référence pour de nombreuses évidences expérimentales observées depuis sa parution.
Je me suis aussi, plus spécialement, intéressé à la résolution des bifurcations de systèmes réversibles (le champ de vecteurs anticommute avec une symétrie), où il apparaît que la forme normale est le plus souvent intégrable. Ces systèmes sont très fréquents en Physique et en Mécanique (voir le chapitre sur la théorie des vagues). Mon travail le plus cité est [49] (1993) avec M.C.Pérouème sur la résonance 1:1  où nous avons pu trouver presqu'explicitement des solutions homoclines alors que les spécialistes se bornaient jusqu'alors à chercher les solutions périodiques. Ce résultat est maintenant utilisé non seulement dans les tiges élastiques, mais aussi dans les systèmes hamiltoniens, comme en optique non linéaire.

Une série de cours faits à Stuttgart en 1990 a engendré le petit livre [M4] (1992), écrit avec M.Adelmeyer (Zurich) et réédité en 1999.  Avec Mariana Haragus (Besançon), nous avons écrit le livre [M5] (329p., Springer UTX series et EDP Sciences, 2011) qui contient toutes les démonstrations pour les variétés centrales et formes normales, et qui contient beaucoup d'exercices et problèmes (résolus) testés dans des cours de DEA à Nice, Bordeaux, Besançon,... Son originalité est de traiter spécifiquement les systèmes de dimension infinie, en donnant les conditions les plus accessibles pour permettre d'utiliser ces techniques, le calcul explicite des formes normales, et comment obtenir les différentes bifurcations, avec un chapitre particulier pour les bifurcations des systèmes réversibles. Dernièrement, avec Mariana Haragus nous montrons [93] l'existence des défauts symétriques dans la convection de Bénard-Rayleigh, ce qui utilise notamment la théorie des formes normales pour un système réversible (ici c'est la direction horizontale x qui joue le rôle du temps), pour montrer l'existence d'une solution hétérocline, connectant les deux régimes de rouleaux symétriques par rapport à 0y. Ces résultats sont complétés dans [95] avec des conditions aux limites mixtes. Enfin le problème des défauts en rouleaux se rencontrant orthogonalement, où les solutions à l'infini ne sont plus symétriques, est traité en collaboration avec B.Buffoni dans [96] par une méthode variationnelle. Ce défaut en rouleaux orthogonaux est maintenant complètement démontré par une étude analytique (technique) [98], [99].

Dans les articles [69] et [74] (2005) avec Eric Lombardi, nous étendons pour des champs de vecteurs analytiques assez généraux, la possibilité de trouver un reste exponentiellement petit, en optimisant le nombre de termes dans la forme normale. Ce type de résultat était seulement connu pour certains champs de vecteurs hamiltoniens. On utilise le même type de technique dans [83] (2009) pour  obtenir des variétés centrales analytiques, à un terme exponentiellement petit près (ce qui permet de simplifier considérablement certaines démonstrations antérieures donnant des solutions avec des "queues" exponentiellement petites). On suggère également des applications en théorie des vibrations non linéaires de structures, où on peut maintenant justifier certaines techniques utilisées par les ingénieurs sous le vocable "modes normaux non linéaires".

Application des méthodes de réductions aux réseaux d'oscillateurs [61], [62], [73], [78]

L'article [61] (2000) avec K.Kirchgässner (Stuttgart) montre que l'on peut utiliser les méthodes de réductions (variété centrale et forme normale) pour l'étude locale des ondes progressives dans les réseaux discrets (infinis) de masses ou d’oscillateurs interagissant avec leur proches voisins (notamment Fermi-Pasta-Ulam, et Klein-Gordon) [61], [62] (2000). La difficulté est de montrer que la réduction à une variété centrale s'applique, malgré l'allure du spectre de l'opérateur linéarisé (commune à tous les réseaux de ce type). Nos résultats ont considérablement enrichi l'ensemble des solutions accessibles analytiquement. L’article de revue [73] (2005) avec G.James fait le point des résultats qui utilisent notre méthode, notamment pour la recherche des "travelling breathers".

Le problème de convection de Bénard-Rayleigh [93], [95], [96], [97], [98], [99]

Mon Directeur de Thèse Jean-pierre Guiraud m'a introduit aux instabilités hydrodynamiques, notamment dans le problème de Couette-Taylor (voir plus haut) et aussi celui de la convection de Bénard-Rayleigh. Il s'agit ici des instabilités d'une couche de fluide visqueux comprise entre deux plans horizontaux, soumise à un chauffage par en dessous, les conditions aux limites pouvant être de 3 types différents: rigide-rigide, rigide-libre ou libre-libre.

Commençant sur la situation "classique", je me suis intéressé déjà en 1977 ([16] avec R.Lozi) au problème Dynamo (création par bifurcation de Hopf d'un champ magnétique lorsque le fluide est conducteur et que la convection est 3-dim) , et me suis aussi intéressé à la convection en fluide compressible [43] (collaboration CEA). Tout récemment, j'ai repris le système des équations de bifurcation pour le problème de convection libre-libre, qui permet des calculs explicites. J'ai ainsi pu montrer [97] que, contrairement aux idées reçues, les seules solutions périodiques bifurquées possiblement stables selon le nombre de Prandtl, sont non seulement les rouleaux bi-dim (classiques) mais aussi le pattern en triangles équilatéraux (plus original, voir la figure plus haut).

Enfin, une série de 5 articles plutôt épais est consacrée à l'étude de certains défauts dans les patterns de convection. Avec Mariana Haragus, nous avons considéré dans un premier temps le défaut où deux régimes de rouleaux se rencontrent symétriquement en faisant un certain angle [93], [95] : ceci utilise la dynamique spatiale, la réduction à une variété centrale de dimension 13, et une mise sous forme normale des termes cubiques, complétée par une étude de persistance d'hétérocline symétrique obtenue sur le système tronqué de dimension 8. Dans un deuxième temps, en collaboration avec Mariana Haragus et Boris Buffoni (EPFL) nous avons considéré le défaut où deux systèmes de rouleaux se rencontrent orthogonalement [96] et montré comment on arrive (via dynamique spatiale, variété centrale et forme normale (encore) en dimension 13 (!)) à un système tronqué de dimension 6 où une méthode variationnelle permet de montrer l'existence de l'hétérocline (non symétrique ici) qui correspond au défaut recherché. J'ai pu ensuite montrer analytiquement l'existence et les propriétés de cette hétérocline [98] et j'ai pu montrer sa persitance pour le système complet de Navier-Stokes-Boussinesq [99], aboutissant à une famille de défauts où les nombres d'onde aux deux infinis diffèrent en général.

Théorie des vagues

J'ai débuté en théorie des vagues vers 1990, influencé par K.Kirchgässner (Stuttgart) et Frédéric Dias (maintenant à Dublin), nouvellement arrivé dans mon labo. Mes derniers résultats sur le Clapotis et sur les vagues tridimensionnelles (symétriques ou non par rapport à la direction de propagation) sont dans 3 articles épais (environ 100p. chacun) comme c'est souvent le cas lorsqu'on résout des problèmes de petits diviseurs.

Application des méthodes de réduction aux vagues [46, 49, 63]

Matisse 1952

Ces articles considèrent le problème des vagues (ondes progressives) bi-dimensionnelles (problème datant de Stokes, il y a plus de 170 ans). On adapte la réduction à une variété centrale, initiée par K.Kirchgässner sur les systèmes elliptiques en domaine cylindrique (on considère la coordonnée d’espace non bornée comme un temps et on traite le problème comme un problème d’évolution, bien que le problème de Cauchy soit mal posé), et on y ajoute la réduction sous forme normale des systèmes réversibles. Nous avons pu prouver [41] (1990) et [49] (1993, cité plus haut) l'existence d'un nouveau type d'onde solitaire, avec des oscillations amorties à l'infini, qui a été une surprise pour les spécialistes, et qui semble être observable dans des circonstances particulières (cf. ref. dans [63]) . Dans [46] (1992)  nous complétons les résultats antérieurement connus, en initiant notamment un important travail sur la bifurcation des ondes solitaires généralisées, ayant une "queue" exponentiellement petite à l'infini (cf. Lecture Notes in Maths 1741 d'E.Lombardi). 
Mes travaux dans ce domaine ont été reconnus d’une part par un prix Max Planck - von Humboldt en 1993 (avec K.Kirchgässner), d’autre part par le privilège (c’en est un pour un mécanicien !) d’une invitation à faire une sectional lecture au Congrès International des Mathématiciens de Berlin en 1998 . L’ensemble des résultats obtenus dans cet état d’esprit (même en vagues 3-dim), a fait l’objet de l’article [63] (2003) de revue écrit avec F.Dias (Cachan) pour le Handbook of Mathematical Fluid Dynamics. Une version courte [C31] a été présentée au Congrès ICM à Berlin.

 Bifurcations de vagues à partir d'un spectre continu [52, 59, 65, 66, 75]

Le problème mathématique de la recherche des ondes progressives est plus difficile lorsqu'une des couches de fluide est d'épaisseur infinie. L'examen des échelles de longueur montre que considérer l'épaisseur comme infinie est pertinent dans la plupart des cas, si l'on souhaite un domaine de validité non négligeable des résultats mathématiques. Une fois formulé comme un système dynamique spatial, on montre que le spectre de l'opérateur linéarisé contient l'axe réel tout entier (spectre essentiel). Ceci empêche l'usage de la réduction à une variété centrale comme ci-dessus. 
J’ai montré que cela ne perturbait pas en général la recherche des ondes progressives périodiques [59] (1999), malgré la résonance due au spectre en 0 (on retrouve ainsi le résultat de Lyapounov - Devaney établi en dimension finie et en l’absence de résonance) (bien que mon résultat soit techniquement simple, il est régulièrement cité).
Nous avons dû construire une théorie de formes normales en présence d'un spectre essentiel réel.  Dans [52] (1996) avec P.Kirrmann (une couche de fluide d'épaisseur infinie, avec tension de surface à la surface libre), nous montrons l'existence d'ondes solitaires avec oscillations amorties à l'infini, mais à décroissance polynomiale, au lieu d'exponentielle comme en profondeur finie. Dans [65] (92p.) et [66] (2002-03) avec E.Lombardi et S.Sun (Virginia Tech) (deux couches superposées, dont une infinie, et tension de surface à la surface libre), nous sommes en présence d'un couplage entre une oscillation naturelle et une décroissance polynomiale lente à l'infini. On montre comment l'équation de Benjamin - Ono apparaît naturellement ici, couplée avec un oscillateur, engendrant la bifurcation d'ondes solitaires généralisées, avec oscillations exponentiellement petites à l'infini. Noter qu'ici, l'effet du spectre essentiel se situe à distance finie, contrairement à [52].  La généralisation de ces études, et l'établissement d'hypothèses génériques, notamment sur la résolvante de l'opérateur linéarisé au voisinage de 0, qui conduisent à ce type de bifurcation est l'objet des travaux de Matthieu Barrandon (thèse en 2004). Un article de revue [75] (2005) écrit avec M.Barrandon fait le point des résultats récents sur ce thème.

Ondes stationnaires de gravité: le Clapotis  [60, 64, 68 (112p.), 71, 72, 80] (avec J.Toland et P.Plotnikov)

Le problème très classique de l’écoulement potentiel bidim périodique en temps et coordonnée horizontale, d'une couche fluide de profondeur infinie, symétrique par rapport à la verticale, avec surface libre et en l’absence de tension de surface, a intéressé notamment Boussinesq (1877) et Rayleigh (1915). La difficulté provient de l'infinité de résonances, et du fait que dans la formulation, les termes non linéaires interviennent avec un ordre de dérivation plus grand que pour les termes linéaires. La note [80] (2007) écrite en l'honneur de Boussinesq, replace son travail séminal dans le cadre actuel.
Dans [60] (1999) et [64] (2002) j'ai simplifié et amélioré les résultats précédents de Toland et Amick (1987) sur l'existence d'une série formelle en puissances de l'amplitude, pour une onde stationnaire, en satisfaisant l'infinité de conditions de compatibilité. De plus, j'ai donné une infinité de solutions différentes, multi-modales à l'ordre principal. Dans [68, 112p.] (2005), complété par [71] et [72], avec P.Plotnikov (Novosibirsk) et J.Toland (Bath), nous arrivons à montrer l'existence des solutions stationnaires unimodale et multimodales, pour des valeurs de l'amplitude dans un ensemble asymptotiquement de mesure pleine à l'origine. Ce travail technique résout, d'une part la difficulté de la dégénérescence complète (noyau de l'opérateur linéarisé de dimension infinie), d'autre part la perte de régularité des termes non linéaires, nécessitant l'application du théorème des fonctions implicites de Nash-Moser. Il faut alors choisir des coordonnées et des variables convenables afin de pouvoir inverser en tout point voisin de 0, la différentielle qui apparaît sous la forme d'une équation hyperbolique non locale en espace, à coefficients périodiques, faisant intervenir un problème de petits diviseurs.

 Vagues de gravité tri-dimensionnelles [M7, 128p.], [84], [85, 87p.] (avec P.Plotnikov)

  Vagues 3-dimensionnelles symétriques (ondes à courtes crêtes). Avec P.Plotnikov [79] (Memoirs of AMS 2009, 128p.), nous avons considéré les ondes progressives bi-périodiques à la surface (libre) d’une couche (infiniment profonde) de fluide parfait en écoulement potentiel, soumise à la seule gravité, qui résultent de l’interaction non linéaire de deux ondes planes périodiques faisant un angle 2ø entre leurs vecteurs d’onde. L’équation de dispersion donne les valeurs critiques µ = cosø du paramètre sans dimension µ (dépend de la longueur d'onde le long de la direction de propagation, et de la vitesse de la vague). Pour les cas non-résonants, on construit formellement une famille d’ondes tri-dimensionnelles, sous la forme de développements en puissances des amplitudes des deux ondes incidentes. Les ondes symétriques par rapport à la direction de propagation (dites "à courtes crètes") sont un cas particulier où les deux amplitudes sont égales. L’objet principal de l'article [79] a été de montrer l’existence de ces solutions symétriques, dont le développement mentionné plus haut constitue le développement asymptotique (figure ci-dessous). La présence de petits diviseurs induit la nécessité de savoir inverser l’opérateur linéarisé en tout point au voisinage de 0, afin d’appliquer le théorème de Nash-Moser. L’opérateur ainsi obtenu est la somme d’un opérateur de dérivation du second ordre dans la direction de la projection horizontale de la vitesse des particules de fluide, et d’un opérateur pseudo-différentiel du premier ordre, tous les deux dépendant périodiquement des coordonnées horizontales. L’inversion d’un tel opérateur est ici la difficulté principale. Les obstacles sont nombreux, notamment la recherche d’un difféomorphisme du tore qui rend constant les principaux coefficients de l’opérateur précédent, le contrôle des petits diviseurs qui nécessite de préciser un résultat d’H.Weyl, et l’implémentation d’une méthode de descente assez générale qui permet de ramener l’inversion de l’opérateur linéaire à l’inversion d’un opérateur de Fredholm. On montre alors que, pour presque tout angle ø, les ondes tri-dimensionnelles bifurquent pour des "bonnes" valeurs de µ dans un ensemble asymptotiquement de mesure pleine au voisinage de la courbe µ = cosø du plan des paramètres. L'infinie régularité de ces solutions périodiques est maintenant démontrée par T.Alazard et G.Métivier, grace à l'utilisation de la technique du calcul paradifférentiel (cf l'article pédagogique sur le sujet paru dans la Gazette des Mathématiciens, en oct 2010). Il est aussi intéressant de noter que la partie principale de ces vagues symétriques correspond exactement aux résultats expérimentaux obtenus notamment par D.Henderson à Penn State en 2005 (voir ref dans [M7]).

  Vagues 3-dimensionnelles asymétriques. Avec P.Plotnikov [84] [85] (ARMA 2010, 87p.), nous prolongeons le résultat précédent au cas des vagues périodiques pour lesquelles le réseau des longueurs d'ondes est non symétrique par rapport à la direction critique de propagation donnée par l'équation de dispersion (la direction de propagation est une des inconnues du problème). On doit, encore ici, trouver un difféomorphisme du tore avec la même propriété que dans le cas précédent pour la différentielle au voisinage de 0, mais avec la difficulté supplémentaire d'avoir à prendre pour le champ des projections horizontales de la vitesse des particules, un nombre de rotation vérifiant une condition diophantienne (d'irrationalité) (alors que ce nombre vaut 1 dans le cas symétrique précédent). Ce difféomorphisme fait alors partie intégrante des inconnues du problème, ainsi que le nombre de rotation, afin d'éviter d'avoir à utiliser une infinité de fois le théorème de Nash-Moser. Nous obtenons alors un résultat similaire au cas symétrique, ici avec les deux amplitudes le long des ondes de bases, ou de façon équivalente, en termes du paramètre µ  et de la direction de propagation, appartenant à un sous ensemble de mesure asymptotiquement pleine au point de bifurcation, ceci pour presque tout (au sens de Lebesque) choix d'angles faits par les deux vecteurs d'onde de base avec l'axe des x (figure ci-dessous).

Une conséquence, intéressante au niveau expérimental (plus difficile à faire), est que pour les solutions précédentes, on montre que dans le référentiel qui est lié aux vagues, la direction moyenne prise par la projection horizontale des trajectoires des particules de fluide à la surface libre, diffère de la direction de propagation des vagues. Il s'agit d'une "dérive directionnelle de Stokes", par analogie au phénomène connu pour les vagues bidimensionnelles, où la vitesse moyenne horizontale des particules est non nulle.