


Next: Topological gradient
Up: Restoration
Previous: Restoration
Contents
Let
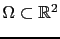 be an open bounded domain, and
be an open bounded domain, and
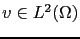 be the noisy image. The enhancement of
be the noisy image. The enhancement of 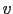 is based on the resolution of the following problem:
is based on the resolution of the following problem:
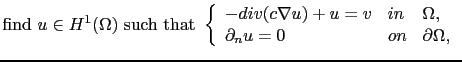 |
(2.21) |
where 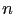 is the outward unit normal to
is the outward unit normal to
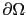 , and
, and 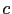 is the conductivity, to be defined in the following. Several choices can be made for the conductivity, mainly
is the conductivity, to be defined in the following. Several choices can be made for the conductivity, mainly 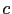 equal to a constant value (linear diffusion method: it is fast, but it blurs important structures), or
equal to a constant value (linear diffusion method: it is fast, but it blurs important structures), or 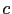 defined by a nonlinear function of
defined by a nonlinear function of 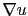 (nonlinear diffusion method, edge-preserving [114,13]). In the topological gradient approach,
(nonlinear diffusion method, edge-preserving [114,13]). In the topological gradient approach, 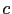 takes only two values: a constant value
takes only two values: a constant value 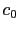 (close to
(close to 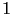 ) in the smooth part of the image, and a very small values
) in the smooth part of the image, and a very small values
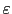 (close to 0
) on the edges or cracks in order to preserve them.
(close to 0
) on the edges or cracks in order to preserve them.
Setting 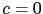 on a part of the image is equivalent to perturbing the domain by the insertion of cracks. For a given point
on a part of the image is equivalent to perturbing the domain by the insertion of cracks. For a given point
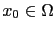 and for a given small parameter
and for a given small parameter 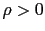 , we consider
, we consider
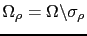 the perturbed domain by the insertion of a crack
the perturbed domain by the insertion of a crack
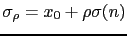 , where
, where 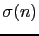 is a straight crack and
is a straight crack and 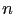 is a unit vector normal to the crack. The variational formulation of the perturbed problem is the following:
is a unit vector normal to the crack. The variational formulation of the perturbed problem is the following:
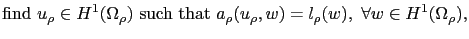 |
(2.22) |
where 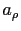 (resp.
(resp. 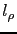 ) is the following bilinear (resp. linear) form defined on
) is the following bilinear (resp. linear) form defined on
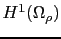 (resp.
(resp.
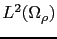 ) by
) by
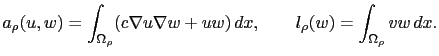 |
(2.23) |
Edge detection if equivalent to looking for a subdomain of 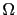 where the energy is small. So our goal is to minimize the energy norm outside edges:
where the energy is small. So our goal is to minimize the energy norm outside edges:
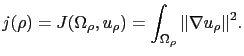 |
(2.24) |



Next: Topological gradient
Up: Restoration
Previous: Restoration
Contents
Back to home page
![]() be an open bounded domain, and
be an open bounded domain, and
![]() be the noisy image. The enhancement of
be the noisy image. The enhancement of ![]() is based on the resolution of the following problem:
is based on the resolution of the following problem:
![]() on a part of the image is equivalent to perturbing the domain by the insertion of cracks. For a given point
on a part of the image is equivalent to perturbing the domain by the insertion of cracks. For a given point
![]() and for a given small parameter
and for a given small parameter ![]() , we consider
, we consider
![]() the perturbed domain by the insertion of a crack
the perturbed domain by the insertion of a crack
![]() , where
, where ![]() is a straight crack and
is a straight crack and ![]() is a unit vector normal to the crack. The variational formulation of the perturbed problem is the following:
is a unit vector normal to the crack. The variational formulation of the perturbed problem is the following:
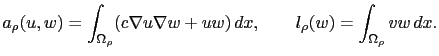
![]() where the energy is small. So our goal is to minimize the energy norm outside edges:
where the energy is small. So our goal is to minimize the energy norm outside edges: