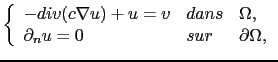


suivant: Gradient conjugué préconditionné
monter: Complexité des algorithmes
précédent: Complexité des algorithmes
Table des matières
Tous les algorithmes que nous avons utilisés reposent sur des résolutions de l'équation
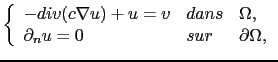 |
(2.54) |
avec différentes valeurs de 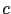 . Les premières résolutions concernent les systèmes direct et adjoint non perturbés, i.e. avec une conductivité
. Les premières résolutions concernent les systèmes direct et adjoint non perturbés, i.e. avec une conductivité 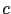 constante. En utilisant une transformée de cosinus discrète (DCT, équivalente à une transformée de Fourier discrète mais en ne gardant que les cosinus), le problème (2.54) est équivalent à résoudre
constante. En utilisant une transformée de cosinus discrète (DCT, équivalente à une transformée de Fourier discrète mais en ne gardant que les cosinus), le problème (2.54) est équivalent à résoudre
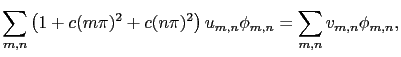 |
(2.55) |
où les fonctions
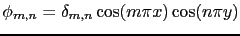 forment une base de cosinus dans
forment une base de cosinus dans
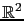 , et où
, et où 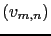 représente les c
représente les c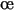 fficients de la DCT de l'image originale
fficients de la DCT de l'image originale 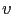 . Par identification dans l'équation (2.55), les c
. Par identification dans l'équation (2.55), les c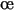 fficients
fficients 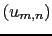 de la DCT de l'image
de la DCT de l'image 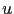 que l'on cherche sont:
que l'on cherche sont:
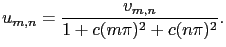 |
(2.56) |
La complexité d'une DCT est
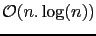 où
où 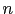 est le nombre de pixels de l'image. La résolution des problèmes non perturbés se fait de la façon suivante:
est le nombre de pixels de l'image. La résolution des problèmes non perturbés se fait de la façon suivante:
- Calcul des c
 fficients
fficients 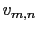 de la DCT de l'image originale
de la DCT de l'image originale 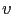 .
.
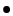
- Calcul des c
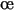 fficients
fficients 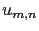 en utilisant (2.56).
en utilisant (2.56).
- Assemblage de l'image
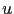 à partir de ses c
à partir de ses c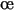 fficients
fficients 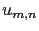 par une DCT inverse.
par une DCT inverse.



suivant: Gradient conjugué préconditionné
monter: Complexité des algorithmes
précédent: Complexité des algorithmes
Table des matières
Retour à la page principale