Corrigé du TP2
1. Simulation de nombres
aléatoires.
x=rand(1,1000);histplot(10,x);xtitle("loi
uniforme")
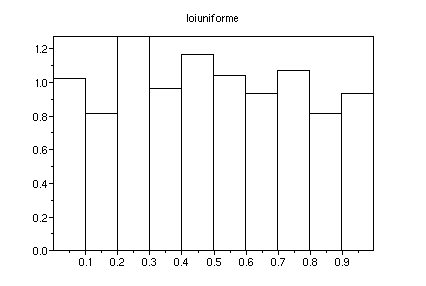
La hauteur du premier baton est donnée par le nombre d'indices i
tels que x(i) est dans l'intervalle [0,0.1] divisé par le
nombre total d'indices et par la largeur de l'intervalle de sorte
que la somme des aires des batons vaut 1 comme l'aire
délimitée par le graphe d'une densité de variable
aléatoire. Idem pour les autres batons.
*On peut contrôler cette affirmation avec la commande sum(bool2s(x<=.1))/(1000*.1)
qui rend ici 1.02. De même sum(bool2s(.2<x
& x<=.3))/(1000*.1) rend 1.26 ce qui correspond à
la hauteur du 3ème batons.*
La valeur attendue est 100/(1000*.1)=1 : on s'attend à ce que le
nombre d'indices i tels que x(i) est dans l'intervalle [0,0.1] soit
proportionnel à la largeur de l'intervalle [0,0.1] si les x(i)
ont été uniformément distribués dans
l'intervalle [0,1].
*Ce n'est pas exactement ce qu'on observe et c'est normal : le nombre
d'indices i tels que x(i) est dans l'intervalle [0,0.1] suit une loi
bionomiale B(1000,1/10) dont l'écart type est
sqrt(1000*1/10*(1-1/10))=9.48.. . Ce nombre divisé par 100 suit
donc une loi proche de la loi normale d'espérance 1 et
d'écart type 0.0948.. . Cet écart-type donne un ordre de
grandeur des fluctuations observées sur la hauteur des batons.
Si au lieu de simuler 1000 nbres aléatoires on en simule 10000,
l'écart type associé à la hauteur d'un des 10
batons devient 0.03. Voici l'histogramme obtenu :
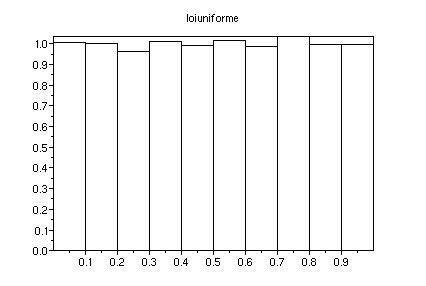 *
*
1.3 2*rand()-1 simule une variable
aléatoire de loi uniforme sur l'intervalle [-1,1]. On peut le
vérifier en définissant un vecteur x comme
précédemment et en traçant l'histogramme
x=2*rand(1,10000)-1;clf();histplot(10,x);xtitle("loi
uniforme sur [-1,1]");xs2gif(0,"hist_unif3.gif")

Pour a<=b, a+(b-a)*rand() simule une va de loi uniforme sur [a,b].
1.4 rand(1,1000,'normal')
définit une matrice 1,1000 (une ligne et 1000 colonnes) dont
chaque élément est obtenu par simulation d'une va de loi
normale N(0,1) (espérance 0 et variance 1). Voici les
histogrammes superposés de x défini par une loi uniforme
et de y défini par une loi normale.
clf();x=rand(1,1000);histplot(10,x)
y=rand(1,1000,'normal');histplot(10,y,style=2)
xtitle("loi uniforme et loi
normale")
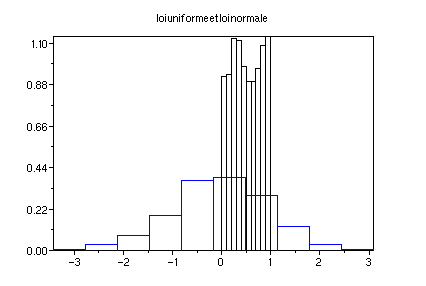
On observe que l'histogramme de x est concentré sur l'intervalle
[0,1] alors que celui de y se réparti sur [-3.5,3]
approximativement. Celui de y est en forme de cloche et est à
peu près symétrique par rapport à 0. Comme
précédemment on peut avoir une meilleure image des lois
uniforme et normale en changeant 1000 en 10000 et on obtient
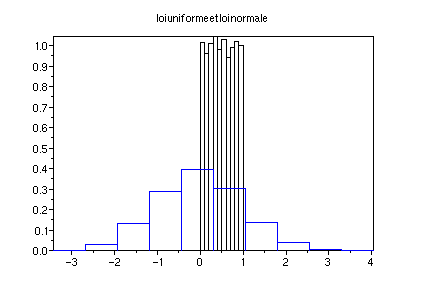
*En fait une va de loi normale N(0,1) est répartie sur R
entier mais la probabilité qu'elle prenne des valeurs hors de
l'intervalle [-4,4] est très faible ce qui fait qu'on ne
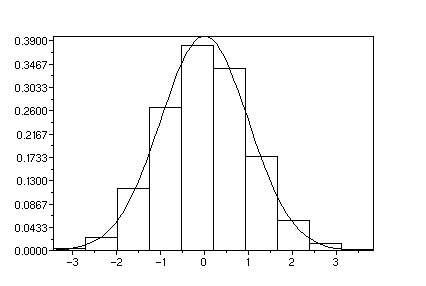
l'observe pas sur l'histogramme. On peut comparer l'histogramme de y
avec la densité de la loi normale
clf();y=rand(1,10000,'normal');histplot(10,y,style=2)
function
y=f(x);y=1/sqrt(2*3.14159)*exp(-x^2/2);endfunction
fplot2d(min(y):.1:max(y),f)
xs2gif(0,"densite-norm.gif")
 *
*
2. Simulation de points
aléatoires dans un carré.
x=2*rand(1,1000)-1;y=2*rand(1,1000)-1;clf();plot2d(x,y,0)
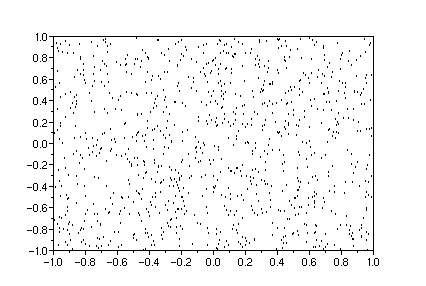
Ca a l'air uniformément réparti.
clf();plot2d(x,x,0)
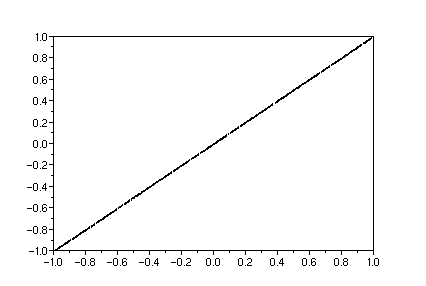
Répartition uniforme sur le segment [(0,0),(1,1)] de R^2.
Si on change y en -y, cela ne changera pas l'allure du nuage (cela
changera le nuage en son symétrique par rapport à la
droite y=0) car la loi de y est symétrique par rapport à
0.
3. Distinguer les points
du disque.
z=bool2s(x^2+y^2<1)
défini un vecteur de même longueur que x et y dont la
i-ème composante vaut 1 si x(i)^2+y(i)^2<1 (c'est à
dire si le couple (x(i),y(i)) est un point du disque D(0,1)), 0 sinon.
clf();for
i=1:1000;plot2d(x(i),y(i),-2*z(i)-2);end
Le dessin met beaucoup plus de temps à ce former que
précédemment. C'est une particularité des boucles
for dans scilab.
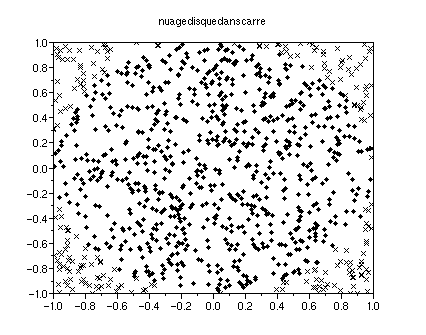
*On peut souvant ruser pour éviter une boucle for.
Essayer ceci :
i=find(x^2+y^2<1);j=find(x^2+y^2>=1)
clf();plot2d(x(i),y(i),-4);plot2d(x(j),y(j),-2)
*
On s'attend à ce que la proportion de points dans le disque soit
égale au rapport de l'aire du disque par l'aire du carré,
c'est à dire pi/4
4. Estimation du nombre pi.
sum(z) rend 784, le nombre
de 1 dans le vecteur z. On en déduit l'approximation
sum(z)*4/1000 = 3.136 de pi. On peut simuler plusieurs fois x et y et
ainsi obtenir de nouvelles approximations :
for
i=1:3;pi(i)=sum(bool2s((2*rand(1,1000)-1)^2+(2*rand(1,1000)-1)^2<1))*4/1000;end
pi'
ce qui donne
! 3.208 2.996 3.144 !
5. Propriétés de
l'estimateur de pi.
On construit un vecteur pi de longueur 400 formé de 400
simulations sucessives de pi par l'instruction
pi=[];for i=1:400;pi(i)=sum(bool2s((2*rand(1,1000)-1)^2+(2*rand(1,1000)-1)^2<1))*4/1000;end
moyenne, écart type, min et max :
[mean(pi),st_deviation(pi),min(pi),max(pi)]
rend ! 3.14357
0.0519110 2.972 3.28 !
clf();histplot(20,pi)
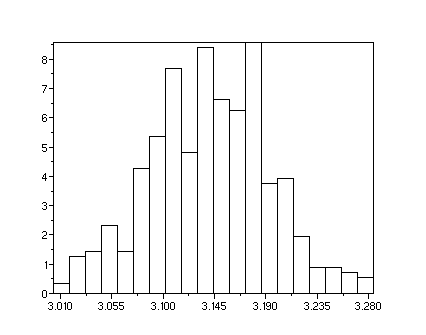
On retrouve sur l'histogramme l'étendue (min et max) et
très approximativement la moyenne. Il est difficile de dire
quelque chose de l'écart-type.
5.3. Soit Z_i la variable
aléatoire qui vaut 1 si le i-ème point est dans le
disque, 0 sinon. Les Z_i sont indépendantes uniformément
distribuées d'espérance m=pi/4 et d'écart-type
sqrt(pi/4*(1-pi/4)). L'espérance de la variable aléatoire
4*(Z_1+...+Z_1000)/1000 est donc pi (linéarité de
l'espérance) et sont écart-type est
4/1000*sqrt(1000*pi/4*(1-pi/4)) ce qui vaut à peu près
0.0519 . On trace la densité de la loi normale N(pi,0.0519)
m=3.14159;s=4/1000*sqrt(1000*m/4*(1-m/4));
function
y=N(x);y=1/(sqrt(2*m)*s)*exp(-(x-m)^2/(2*s*s));endfunction
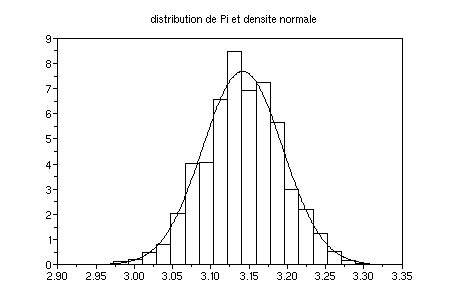
clf();fplot2d(min(pi):.01:max(pi),N)
xtitle("distribution de Pi et
densite normale")
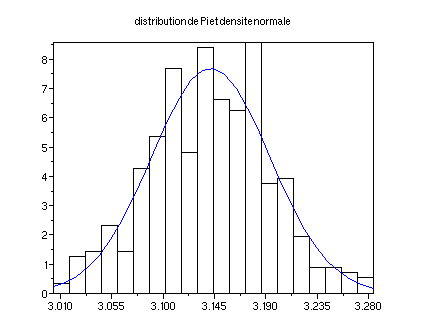
On observe des fluctuations des hauteurs des batons autour des valeurs
prédites par le graphe de N.
6. Contrôle de la
règle des 95%.
Les bornes de l'intervalle I_2sigma sont données par
l'instruction
[m-2*s,m+2*s] qui
rend ! 3.0377291 3.2454509 !
Celles de I_sigma sont données par
[m-s,m+s] qui rend
! 3.0896595 3.1935205 !
On compte le pourcentage d'indices i tel que pi(i) n'est pas dans
I_2sigma :
mean(bool2s(m-2*s<pi &
pi<m+2*s)) rend 0.965
mean(bool2s(m-s<pi &
pi<m+s)) rend 0.67
7. Influence de la taille
de l'échantillon sur la qualité de l'estimateur.
On définit successivement un vecteur pi de longeur 400 puis 40
puis 4000 :
Pi(1:400) :
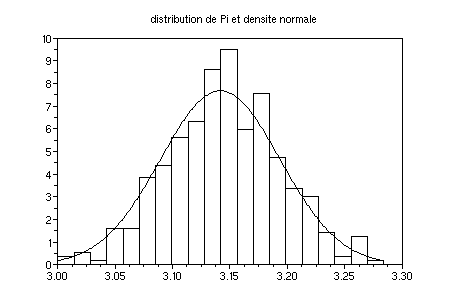
Pi(1:40) avec le script :
n1=40;//40 400 4000
n2=1000;//1000 10000
pi=[,];for
i=1:n1;x=2*rand(1,n2)-1;y=2*rand(1,n2)-1;pi(i)=4*sum(bool2s(x^2+y^2<1))/n2;end
clf();histplot(20,pi);
m=3.14159,sigma=4*sqrt(m*(4-m))/(4*sqrt(n2))
function
y=n(x);y=1/(sigma*sqrt(2*m))*exp(-(x-m)^2/(2*sigma^2));endfunction
fplot2d(min(pi):.001:max(pi),n)
xtitle("distribution de Pi et
densite normale")
[m-sigma,m+sigma]
[m-2*sigma,m+2*sigma]
mean(bool2s(m-sigma<pi &
pi<m+sigma))
mean(bool2s(m-2*sigma<pi &
pi<m+2*sigma))
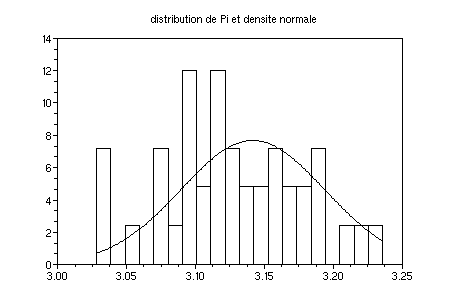
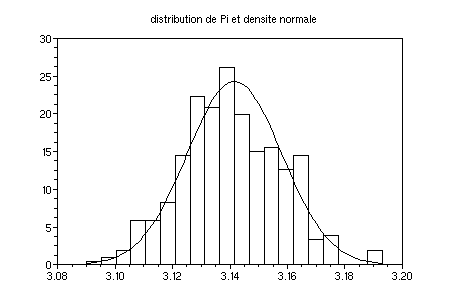
Pi(1:4000) :
Pi(1:400), chaque valeur de Pi étant calculée avec 10000
itérations au lieu de 1000 :

 *
*


 *
*







