corr TP3

Corrigé du TP3

FX Dehon, 18 avril 2006

1. Fluctuation d'échantillonnage.
1.1 p=0.4
rand()+p rend un nombre, disons x, de l'intervalle [p,1+p] suivant la loi uniforme. Puisque 0<=p<1, int(x) rend 0 si x est dans l'intervalle [p,1[ et 1 si x est dans l'intervalle [1,1+p]. La probabilité que x soit dans l'intervalle [1,1+p] est le rapport entre la longueur de l'intervalle [1,1+p] et celle de [p,1+p], c'est à dire p.

n=400;sondages=int(rand(1,n)+p);fe=sum(sondage)/n
rend 39.805

On peut afficher 4 valeurs consécutives par l'instruction
fe=[];for i=1:4;fe(i)=sum(int(rand(1,n)+p))/n;end;fe'
ce qui donne
0.4275 0.3925 0.38 0.395

La valeur théorique est l'espérance de la variable aléatoire fe, qui vaut p=0.4.

1.2 grand(1,n,'bin',1,p) donne un résultat équivalent à int(rand(1,n)+p) mais calculé suivant un algorithme différent (faire help grand).

1.3
m=100;sondages=int(rand(m,n)+p);fe=sum(sondages,'c')/n
définit un vecteur colonne fe de longeur 100 avec pour tout 1<=i<=100 fe(i) est la moyenne des valeurs de la ligne i de fe. C'est le sens de l'argument 'c' dans l'instruction sum

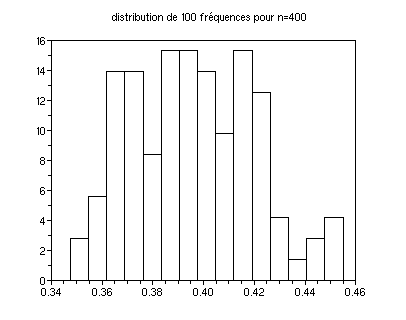
Histogramme en 15 classes :
clf();histplot(15,fe)
xtitle("distribution de "+string(m)+" fréquences pour n="+string(n)) // donne un titre indiquant m et n
xs2gif(0,"hist_"+string(m)+"x"+string(n)+".gif") // sauvegarde l'image dans un fichier GIF.

2. Position et étendue de fe.
2.1 [mean(fe),median(fe)] rend 0.4013 0.405
Ces deux valeurs ne sont pas égales mais diffèrent de peu ce qui traduit le fait que la distribution de fe est proche d'une distribution symétrique par rapport à l'espérance 0.4.

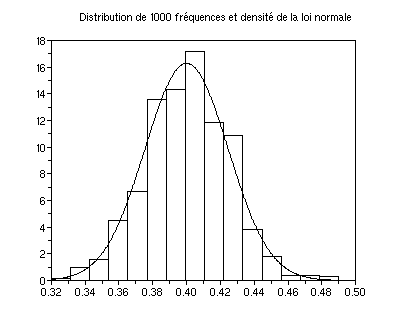
*En fait si on prend m grand, la distribution (empirique) de fe devient proche de celle d'une loi normale N(0.4, 0.024) (l'écart type théorique de fe est sqrt(0.4*(1-0.4)/n)=0.024..). En voici l'illustration en prenant m=1000 :
m=1000;n=400;fe=sum(int(rand(m,n)+p),'c')/n;
clf();histplot(15,fe)
sig=sqrt(.4*.6/n);function y=N(x);y=1/(sig*sqrt(2*3.14159))*exp(-(x-.4)^2/(2*sig^2));endfunction;
fplot2d([min(fe):(max(fe)-min(fe))/500:max(fe)],N)
xtitle("Distribution de "+string(m)+" fréquences et densité de la loi normale")
xs2gif(0,"hist_"+string(m)+"-dens.gif")

*
2.2 On revient à notre vecteur fe de longueur m=100
q=quart(fe);[max(fe)-min(fe),stdev(fe),q(3)-q(1)] donne 0.125 0.0241967 0.03375
Ces valeurs diffèrent mais les deux dernières sont du même ordre de grandeur. Si on approxime la distribution de fe par celle d'une loi normale d'espérance 0.4 et d'écart type sigma=sqrt(.4*.6/n) (=0.024..) on aurait q(3)-q(1)=0.67*sigma (essayer l'instruction cdfnor("X",0,1,.75,.25)). C'est la longueur de l'intervalle de confiance à 50%.

2.3. length(fe(min(fe)<=fe & fe < max(fe))) rend 99 parce que fe atteint exactement une fois la valeur max(fe) et max(fe) est exclu de l'intervalle.
length(fe(q(1)<=fe & fe < q(3))) rend 47. On s'attend à 50. Pour expliquer l'écart (raisonable) on peut analyser le vecteur f=sort(fe). q(1) est (pour la présente exécution du script) entre la 75ème et la 76ème valeur de f dans l'ordre décroissant ; q(3) est la valeur commune de f (23),..,f(28) et cette valeur est exclue de l'intervalle.

2.4. sqrt(p*(1-p)/n) est l'écart type de la variable aléatoire fe. Il dépend de la loi suivant laquelle fe est simulée mais pas des valeurs particulières prises par fe contrairement à l'écart type empirique. On trouve 0.0244949 ce qui est proche de l'écart type empirique calculé en question 2.2.

*On pourrait calculer l'écart type théorique de la variable aléatoire dont la réalisation est l'écart type empirique et en déduire un intervalle de confiance à 95% pour l'écart type empirique.
Faisons le pour la variance empirique : celle-ci est donnée par la formule ((fe(1)-p)^2+...+(fe(m)-p)^2)/m dont la variance théorique est Var((fe-p)^2)/m=1/m*(E((fe-p)^4)-(np(1-p))^2).
...
*

3. Intervalle de confiance.
sigma=sqrt(p*(1-p)/n)
feinf=fe-1.96*sigma;fesup=fe+1.96*sigma;ftheo=p*ones(m,1);
définit trois vecteurs de longueur m.
ones(m,1) rend une matrice de m lignes et 1 colonne, valant 1 en chaque position.

3.2. On peut faire un dessin plus parlant :
clf();for i=1:m;plot2d([i,i],[feinf(i),fesup(i)],style=1);end
plot2d([0,m],[p,p],style=1)
xs2gif(0,'int_conf.gif')

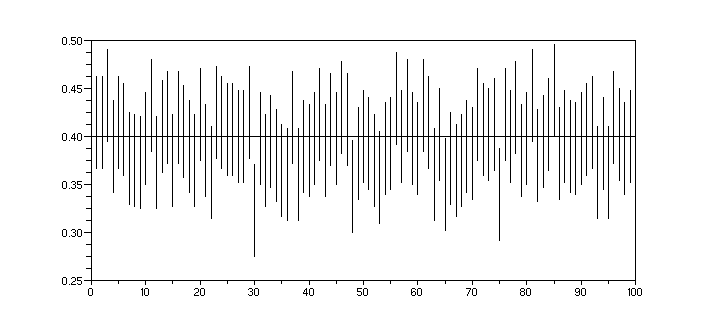
On observe sur la figure 4 (ou peut être 5) intervalles ne contenant pas p.

3.3 On peut calculer ce nombre d'intervalle par l'instruction
length(fe(p<feinf | p>fesup)) ou encore par l'instruction sum(bool2s(p<feinf | p>fesup))
qui rendent 4.
La valeur attendue est 5 (p est dans l'intervalle de confiance avec une probabilité de 95%). Il y a des fluctuations autour de cette valeur attendue et en fait on pourrait calculer un intervalle de confiance sur le nombre trouvé d'intervalles ne contenant pas p. Voir le commentaire de la question 4.6.

3.4 Pour des intervalles de confiance à 10% :
feinf=fe-1.64*sigma;fesup=fe+1.64*sigma; //(cf cours)
clf();for i=1:m;plot2d([i,i],[feinf(i),fesup(i)],style=1);end
plot2d([0,m],[p,p],style=1)
xs2gif(0,'int_conf10.gif')

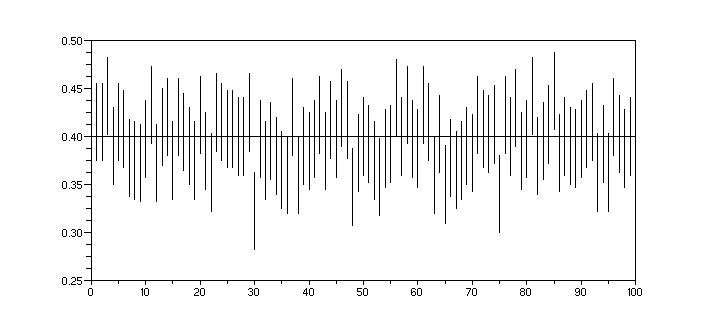
Les intervalles sont de longueur plus petite mais davantage ne contiennent pas p.
length(fe(p<feinf | p>fesup))
et on obtient 8. La valeur attendue est 10.

4. Influence de la taille de l'échantillon.
4.1
n=1000;sigma=sqrt(p*(1-p)/n);fe=sum(int(rand(1,n)+p),'c')/n;
[fe,fe-1.96*sigma,fe+1.96*sigma]
ans =

0.418 0.3876358 0.4483642
[fe-1.64*sigma,fe+1.64*sigma]
ans =

0.3925932 0.4434068
4.2
m=100;fe=sum(int(rand(m,n)+p),'c')/n;
clf();histplot(15,fe)
xtitle("Distribution de "+string(m)+" fréquences pour n="+string(n))
xs2gif(0,"hist_"+string(m)+"x"+string(n)+".gif")

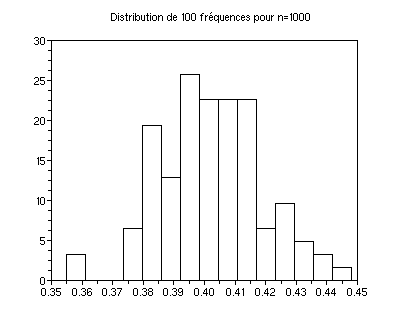
L'histogramme montre une distribution plus serrée autour de la moyenne. On ne peut pas dire grand chose sur sa forme parce que m=100 est trop petit.

4.3 La moyenne théorique de fe est toujours p=0.4 . mean(fe) rend 0.40199

4.4 L'écart type théorique vaut maintenant 0.0154919. stdev(fe) rend 0.0166621

4.5
[length(fe(p<fe-1.96*sigma | p>fe+1.96*sigma)),length(fe(p<fe-1.64*sigma | p>fe+1.64*sigma))]
rend
7. 13.
Les valeurs attendues sont toujours 5 et 10. On note une forte variabilité. Voir le commentaire plus loin.

4.6 On change quelque peu la définition de fe :
n=10000;sigma=sqrt(p*(1-p)/n);fe=grand(m,1,'bin',n,p)/n;
[length(fe(p<fe-1.96*sigma | p>fe+1.96*sigma)),length(fe(p<fe-1.64*sigma | p>fe+1.64*sigma))]
rend
4. 15.

*Voici les histogrammes de 1000 calculs du nombre d'intervalles ne contenant pas p pour alpha=5%, n=400 puis n=10000 :
m=100;n=400;sigma=sqrt(p*(1-p)/n);l=[];for i=1:1000;fe=grand(m,1,'bin',n,p)/n;
l(i,:)=[length(fe(p<fe-1.96*sigma | p>fe+1.96*sigma)),length(fe(p<fe-1.64*sigma | p>fe+1.64*sigma))];
end;
clf();histplot([.5:15.5],l(:,1),rect=[0,0,15,.22]);xtitle("Nombre d intervalles au seuil 5% ne contenant pas p pour n="+string(n))
xs2gif(0,"hist_int_"+string(n)+".gif")

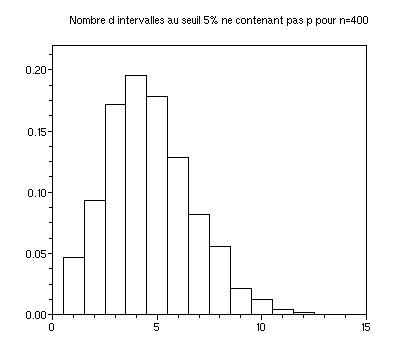
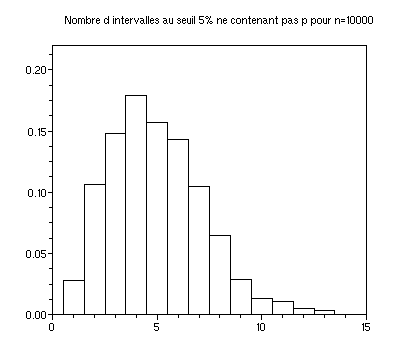
Les deux histogrammes sont très semblables. Voici une explication :
Si les bornes de l'intervalle de confiance pour fe sont optimales, le nombre d'intervalles au seuil alpha ne contenant pas p suit une loi binomiale B(m,alpha) d'écart type s=sqrt(m*alpha*(1-alpha))=
2.179.. pour m=100 et alpha=5%,
3 pour m=100 et alpha=10%.
Avec la fonction de répartition de la loi binomiale (help cdfbin) on obtient par exemple que la probabilité que le nombre calculé soit supérieur à alpha+s est de 11% pour alpha=5% et de 12% pour alpha=10%. (On notera que le rapport s/alpha tend vers l'infini quand alpha tend vers 0.).
La variabilité ainsi exprimée ne dépend que de m et alpha, pas de n.
*