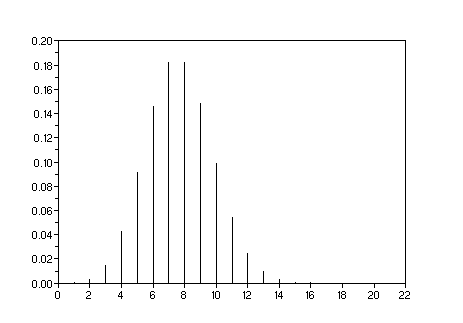TP4
1.a.
p=1/3;mean(bool2s(rand(1:1000)<p))
sig=sqrt(p*(1-p))/sqrt(1000) //ecart type de la moyenne de 1000 bernouilli iid p
0.327
0.0149071
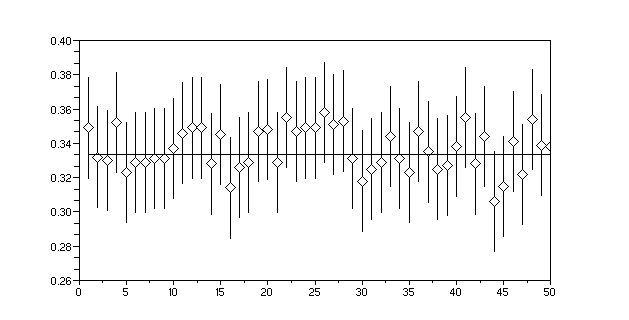
J'obtient pour moyenne 0.327, intervalle de confiance
[m-1.96*sig,m+1.96*sig]=[0.298,0.356] de longueur 2*.03. Voici la
représentation graphique de 50 moyennes calculées avec
leurs intervalles de confiance :
clf();n=50;for i=1:n
y=mean(bool2s(rand(1:1000)<p)); //mean(grand(1,1000,'bin',1,p))
plot2d([i,i],[y-sig*1.96,y+sig*1.96],style=1);
plot2d(i,y,-5);
end;
plot2d([1,n],[p,p],style=1)
La proportion d'intervalles ne contenant pas p peut être simulée par l'instruction
n=100;
f=[,];for i=1:n;f(i)=mean(bool2s(rand(1:1000)<p));end;
mean(bool2s(f-1.96*sig<p & p<f+1.96*sig))
qui donne après plusieurs exécutions successives
0.98 0.94
0.98 0.98 0.96
0.94 0.94 0.95
0.93 0.91
Il y a des fluctuation et c'est normal puisque l'intervalle de
confiance à 95% pour la va de bernouilli
"f est dans
[p-1.96*sig,p+1.96*sig]"
est de longueur
2*1.96*sqrt(0.05*0.95)/sqrt(100) = 0.043 .
Avec n=10000, la longueur devient 0.0043 et on obtient pour les 10 premières valeurs simulées
0.9472 0.9479
0.9488 0.9493
0.948 0.9508 0.9518
0.9498 0.9496 0.9501
(n=10000;t=[,];f=[,];sig2=1.96*sig;for j=1:10;
for i=1:n;f(i)=mean(bool2s(rand(1:1000)<p));end;
t(j)=mean(bool2s(f-sig2<p & p<f+sig2));end;t')
1.b. b=binomial(p,20);clf();plot2d3(b)
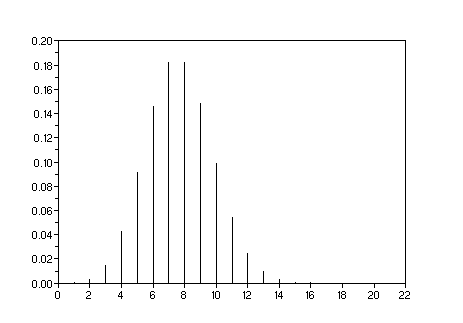
s=[,];for i=1:1000;s(i)=sum(bool2s(rand(1:20)<p));end
xset("window",1);clf();histplot([0.5:20],s)
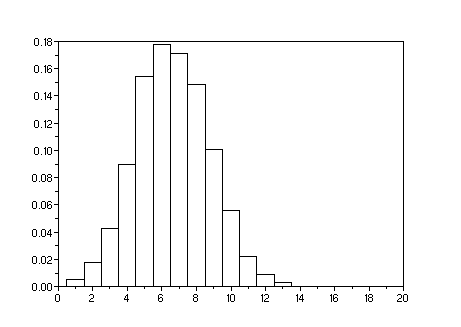
Avec 50 itérations au lieu de 1000, on obtient par exemple ceci
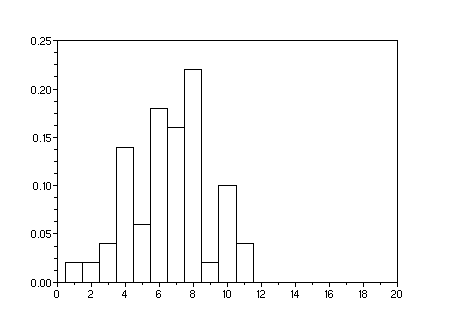
1.c.
f=[,];for i=1:21;f(i)=sum(b(1:i));end
xset("window",2);plot2d2([0:20],f)
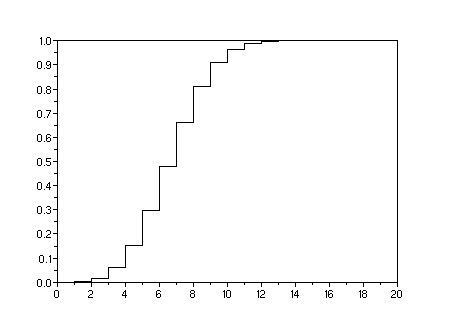
1.d. P(S>=10)=1-P(S<=9)=1-f(10). L'instruction
for r=[2,3,5],b=binomial(1/r,20);for i=1:21;f(i)=sum(b(1:i));end;1-f(10),end
rend
0.588 0.0918 0.00259
correspondant à p=1/2, 1/3 et 1/5 respectivement.
On peut le faire 10 fois de suite comme suit :
m=[,];for k=1:10;
for r=[2,3,5];
s=[,];for i=1:1000;s(i)=sum(bool2s(rand(1:20)<1/r));end;
m(k,r)=mean(bool2s(s>=10));
end;
end;
m(:,[2,3,5])
ans =
0.577 0.092 0.005
0.595 0.085 0.002
0.579 0.084 0.003
0.587 0.09 0.005
0.571 0.091 0.002
0.586 0.085 0.002
0.589 0.082 0.
0.586 0.104 0.002
0.594 0.103 0.003
0.59 0.087 0.004
1.e. L'instruction
f=[,];for r=[2,3,5,10];b=binomial(1/r,20);for i=1:21;f(i,r)=sum(b(1:i));end;end;
[[0:20]',f(:,[2,3,5,10])]
produit le tableau donné.
pour r=2,3,5,10, l'instruction find(1-f(:,r)<=.05,1)
rend le premier indice i>=1 tel que P(S>i-1)=1-f(i,r)<=.5
(attention au décalage d'indice). La suite des k(r)=k_{1/r}
cherchée est donnée par
k=[,];for r=[2,3,5,10];k(r)=find(1-f(:,r)<=.05,1)-1;end;k([2,3,5,10])'
et on obtient
14. 10. 7. 4.
2. b. On veut P(S>1/r+delta)<=5%. Il faut et il suffit d'avoir 1/r+delta>=k_{1/r}. On obtient
delta_2 >= 13.5
delta_3 >= 9.66..
delta_5 >= 6.8
delta_10 >= 3.9
2.c. On cherche P(S<=k_{1/r}) pour p=2/3 ce que donne sum(b(1:kr)) une fois redéfini b.
b=binomial(2/3,20);e=[,];for r=[2,3,5,10];e(r)=sum(b(1:k(r)));end;e([2,3,5,10])'
et on obtient
0.7027861 0.0918958 0.0037246 0.0000251
2.d. On cherche k tel que P(S<=k) soit inférieur à 5%
sachant p=2/3. On peut afficher les valeurs de la fonction de
répartition de la binomiale B(20,2/3) par l'instruction
f1=[,];b=binomial(2/3,20);for i=1:21;f1(i)=sum(b(1:i));end;[[0:20]',f1]
et y lire la valeur de k.
! 0. 2.868D-10 !
! 1. 1.176D-08 !
! 2. 0.0000002 !
! 3. 0.0000028 !
! 4. 0.0000251 !
! 5. 0.0001674 !
! 6. 0.0008788 !
! 7. 0.0037246 !
! 8. 0.0129733 !
! 9. 0.0376366 !
! 10. 0.0918958 !
! 11. 0.1905489 !
! 12. 0.3385285 !
! 13. 0.5206573 !
! 14. 0.7027861 !
! 15. 0.8484891 !
! 16. 0.9395535 !
! 17. 0.9824074 !
! 18. 0.9966920 !
! 19. 0.9996993 !
! 20. 1. !
On obtient k=9. Il faut donc 1/r+delta <= 9.
Pour r=2,3,5,10 on trouve
delta=[,];for r=[2,3,5,10];delta(r)=9-1/r;end;delta([2,3,5,10])'
8.5 8.66.. 8.8 8.9
A partir de r=5 c'est compatible avec les exigences de 2.b.
3.
r=3;N=500;
p=[ones(N,1)*1/r;ones(N,1)*2/3]; //colonne de longueur 2N
mp=p;for i=1:19;mp=[mp,p];end; //matrice formee de 20 repetitions de p
t=[,];copies=[,];s=[,];for i=1:10;// 10 simulations
copies=bool2s(rand(ones(2*N,20))<mp); //matrice 2Nx20 formee de bernouilli p(i)
s=copies*ones(20,1);
t(i,1)=sum(bool2s(s(1:500)>k(r)));t(i,2)=sum(bool2s(s(501:1000)<=k(r)));
end;t
rend le nombre de copies rejetées parmis les 500
premières suivi du nombre de copies non rejetées parmis
les 500 dernières.
! 24. 52. !
! 23. 52. !
! 14. 43. !
! 16. 39. !
! 20. 44. !
! 18. 50. !
! 27. 45. !
! 23. 51. !
! 19. 47. !
! 14. 44. !
La première colonne est conforme au prévision. La
deuxième colonne indique un taux de non-rejet
d'élèves n'ayant pas répondu au hasard de
10% environ. On a k_{1/3}=10. La réponse à la question
2.c prévoit un taux de non rejet pour les 500 dernières
copies de 9%.
Avec r=5
! 15. 0. !
! 10. 1. !
! 13. 1. !
! 12. 2. !
! 13. 3. !
! 22. 3. !
! 12. 1. !
! 23. 2. !
! 20. 2. !
! 20. 4. !
On reste avec un taux de rejet à tort parmis les 500
premières copies de l'ordre de 5% (par construction de k_{1/5}=7
: la fonction de répartition de S permet de prévoir en
fait un taux de rejet à tort de 3.2%). Le taux de non rejet des
500 dernières est nettement meilleur qu'avec r=3. Le taux de non
rejet prévu à la question 2.c est 0.37%.
Remarques :
- Fluctuation du nombre de rejets parmis les 500 dernières copies pour r=5 :
r=5;N=500;
nn=100;
t=[,];copies=[,];s=[,];for i=1:nn;// nn simulations
copies=bool2s(rand(ones(N,20))<2/3); //matrice Nx20 formee de bernouilli 2/3
s=copies*ones(20,1);
t(i)=sum(bool2s(s(1:500)<=k(r)));
end;
clf();plot2d(t)
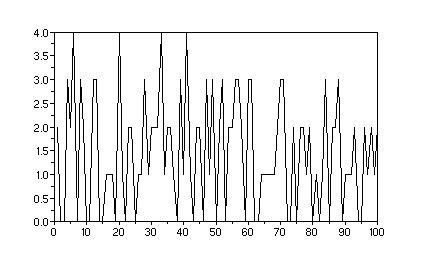
L'écart entre les valeurs est de l'ordre de grandeur des valeurs. Pourquoi ?
- Un script plus efficace :
mean(bool2s(grand(1,500,'bin',20,2/3)<=k(r))) //taux de non rejet sur un paquet de 500 copies 2/3
mean(bool2s(grand(1,10*500,'bin',20,2/3)<=k(5))) //taux de non rejet apres 10 simulations
mean(bool2s(grand(1,100*500,'bin',20,2/3)<=k(5))) //taux de non rejet apres 100 simulations