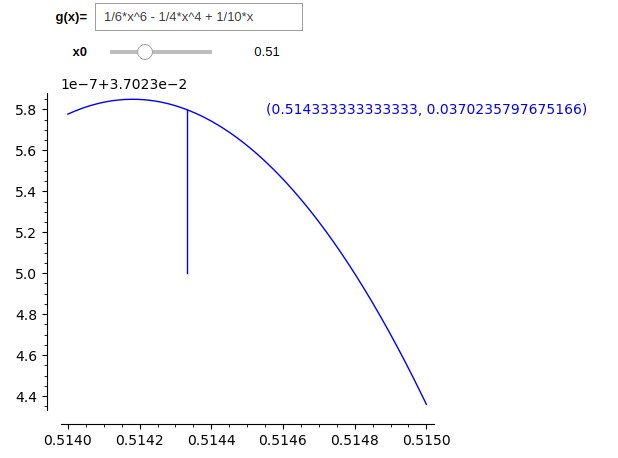
a,b,ymin=0.514,.515,0.0370235
@interact
def go(g=input_box(1/6*x^6-1/4*x^4+1/10*x,label='g(x)='),x0=slider(a,b,(b-a)/100,default = a*2/3+b*1/3)):
g(x)=g(x=x)
p1=plot(g,(x,a,b))
p2=line([(x0,ymin),(x0,g(x0))])
show(p1+p2+text(str((x0,g(x0))),(b,g(x0))))
Conclusion : max atteint sur l'intervalle
Points d'annulation de la dérivée :
g(x)=1/6*x^6-1/4*x^4+1/10*x
dg(x)=diff(g(x),x)
show("g'(x)=",dg(x))
#Alternative
show("gradiant de g en x = vecteur de ℝ = nombre réel :",g.gradient()(x))
g(x)=1/6*x^6-1/4*x^4+1/10*x
dg(x)=diff(g(x),x)
show("g'(x)=",dg(x))
sol=solve(dg==0,x,to_poly_solve='force')
show("g'(x)=0 pour x= :")
for s in sol:
show(s.rhs())
On obtient comme points d'annulation de : et deux nombres complexes qu'on ignore.
Rq: La liste obtenue avec Sagemath est exhaustive car est une fonction polynomiale de degré 5 ; elle s'annule en au plus points et Sagemath en a trouvé 5.
On compare avec le graphe de :
plot(g,-1.4,1.2)
Sur le graphe correspond à un minimum local (peut être global) de , correspond à un max local mais pas global, correspond à un min local mais pas global.
Rq. Après coup est un minimum global, sinon devrait changer de sens de variation en dehors de l'intervalle représenté mais alors s'annulerait en au moins un 6-ème point, impossible puisque est une fonction polynomiale de degré .
dxL(x,k,l)=diff(g(x)-k*(-x)-l*(x-1),x)
s=solve([dxL(x,k,l)==0,k*(-x)==0,l*(x-1)==0],[x,k,l])
for i in range(len(s)):
print(i+1,s[i])
1 [x == -1.043122035360069, k == 0.0, l == 0.0] 2 [x == 0.9373188405797102, k == 0.0, l == 0.0] 3 [x == (-0.2041887771764046 - 0.3965088043695821*I), k == 0.0, l == 0.0] 4 [x == (-0.2041887771764046 + 0.3965088043695821*I), k == 0.0, l == 0.0] 5 [x == 0.5141808475141808, k == 0.0, l == 0.0] 6 [x == 0, k == (-1/10), l == 0] 7 [x == 1, k == 0, l == (1/10)]
On retient les solutions 2,5,7. Les autres sont soit hors domaine , soit avec des multiplicateurs de Lagrange pas tous positifs.
On compare les valeurs de en ces solutions :
for i in [2,5,7]:
x=s[i-1][0].rhs()
print(i,"x=",x.n(digits=3),"\t g(x)=",g(x).n())#i-1 car l'indentation des listes commence à 0 en Python
#.n() pour afficher une valeur numérique
2 x= 0.937 g(x)= 0.0137866236594794 5 x= 0.514 g(x)= 0.0370235849280557 7 x= 1.00 g(x)= 0.0166666666666667
On peut même demander à Sagemath de faire cette comparaison :
m=max([g(s[i-1][0].rhs()) for i in [2,5,7]])
for i in [2,5,7]:
x=s[i-1][0].rhs()
if g(x)==m:print("sol no",i,", x=",x)
sol no 5 , x= 0.5141808475141808
Les candidats pour la recherche du minimum de sur le même intervalle sont les annulant le Lagrangien tels que et (gradiant rentrant).
On retient les solutions 2,5,6. On distingue ces solutions comme précédemment en calculant les valeurs de en les points correpondants :
for i in [2,5,6]:
x=s[i-1][0].rhs()
print(i,"x=",x.n(digits=3),"\t g(x)=",g(x).n())
2 x= 0.937 g(x)= 0.0137866236594794 5 x= 0.514 g(x)= 0.0370235849280557 6 x= 0.000 g(x)= 0.000000000000000
C'est la solution no 6 qui est qualifiée.
var('k l m r')
U(x,y)=(x+2)*(x+3*y)
c1(x,y)=-x
c2(x,y)=-y
c3(x,y)=5*x+3*y-r
L(x,y)=U(x,y)-k*c1(x,y)-l*c2(x,y)-m*c3(x,y,r)
dL(x,y)=(diff(L(x,y),x),diff(L(x,y),y))
show("gradiant du Lagrangien :",dL(x,y))
#Alternative
print(dL(x,y)==L.gradient()(x,y))
#Rq f(x,y)=dL(x,y) produit une erreur !
True
On commence avec :
r0=20
var('x y k l m')#ces variables ne doivent pas avoir de valeur pour l'instruction ci-dessous
sol=solve([dL(x,y)[0]==0,dL(x,y)[1]==0,k*c1(x,y)==0,l*c2(x,y)==0,m*c3(x,y,r=r0)==0],[x,y,k,l,m])
for i in range(len(sol)):
print(i+1,sol[i])
1 [x == -2, y == (2/3), k == 0, l == 0, m == 0] 2 [x == -1, y == 0, k == 0, l == -3, m == 0] 3 [x == 0, y == 0, k == -2, l == -6, m == 0] 4 [x == (3/2), y == (25/6), k == 0, l == 0, m == (7/2)] 5 [x == 0, y == (20/3), k == -12, l == 0, m == 2] 6 [x == 4, y == 0, k == 0, l == -12, m == 2]
On peut filtrer les solutions en ne retenant que celles pour lesquelles vérifient les contraintes et les multiplicateurs de Lagrange sont :
for i in range(len(sol)):
x,y,k,l,m=(s.rhs() for s in sol[i])
if c1(x,y)<=0 and c2(x,y)<=0 and c3(x,y,r=r0)<=0 and k>=0 and l>=0 and m>=0:
print(i,sol[i])
3 [x == (3/2), y == (25/6), k == 0, l == 0, m == (7/2)]
Les contraintes pour lesquelles le multiplicateur est non nul sont forcément saturées (puisque le produit est nul).
On a donc pour une seule solution , laquelle est sur la droite formée par la saturation de la contrainte de budget.
Pour r=5 maintenant :
r0=5
var('x y k l m')
sol=solve([dL(x,y)[0]==0,dL(x,y)[1]==0,k*c1(x,y)==0,l*c2(x,y)==0,m*c3(x,y,r=r0)==0],[x,y,k,l,m])
for i in range(len(sol)):
print(i+1,sol[i])
print("\nSolution qualifiée :")
for i in range(len(sol)):
x,y,k,l,m=(s.rhs() for s in sol[i])
if c1(x,y)<=0 and c2(x,y)<=0 and c3(x,y,r=r0)<=0 and k>=0 and l>=0 and m>=0:
print(i+1,sol[i])
1 [x == -2, y == (2/3), k == 0, l == 0, m == 0] 2 [x == -1, y == 0, k == 0, l == -3, m == 0] 3 [x == 0, y == 0, k == -2, l == -6, m == 0] 4 [x == (-3/8), y == (55/24), k == 0, l == 0, m == (13/8)] 5 [x == 0, y == (5/3), k == 3, l == 0, m == 2] 6 [x == 1, y == 0, k == 0, l == (-33/5), m == (4/5)] Solution qualifiée : 5 [x == 0, y == (5/3), k == 3, l == 0, m == 2]
Cette fois les deux contraintes et sont saturées : on se trouve à un coin du domaine.
Comme les expressions de la fonction d'utilité et des contraintes de budget sont simples, on peut demander à Sagemath les solutions (non filtrées !) en fonction du paramètre :
var('x y k l m r')
sol=solve([dL(x,y)[0]==0,dL(x,y)[1]==0,k*c1(x,y)==0,l*c2(x,y)==0,m*c3(x,y,r)==0],[x,y,k,l,m])
for i in range(len(sol)):
print(i+1,sol[i])
1 [x == -2, y == (2/3), k == 0, l == 0, m == 0] 2 [x == -1, y == 0, k == 0, l == -3, m == 0] 3 [x == 0, y == 0, k == -2, l == -6, m == 0] 4 [x == 1/8*r - 1, y == 1/8*r + 5/3, k == 0, l == 0, m == 1/8*r + 1] 5 [x == 0, y == 1/3*r, k == -r + 8, l == 0, m == 2] 6 [x == 1/5*r, y == 0, k == 0, l == -9/25*r - 24/5, m == 2/25*r + 2/5]
On peut même demander la discussion en posant les bonnes questions :
var('r')
for i in range(len(sol)):
x,y,k,l,m=(s.rhs() for s in sol[i])#Attention à l'indentation
show(i+1,solve([c1(x,y)<=0,c2(x,y)<=0,c3(x,y,r)<=0,k>=0,l>=0,m>=0],[r]))