Scilab
et la dynamique de l'approximation diophantienne d'un réel
Scilab cf help('int'), etc
Etude du système dynamique x -> 1/(x-int(x)) sur
[1,\infty[\Q
ou de façon equivalente x \mapsto 1/x - int(1/x) sur
[0,1]\Q.
C'est ce dernier qu'on représente graphiquement.
Le calcul du spectre de matrices 2x2 de la forme [k,1;1,0] ou d'un
produit de matrices de cette forme sert à trouver les points
fixes de l'extension à P^1(R) d'une section de f ou d'une
composée de telles sections, ce qui donne des points fixes
de f
ou de composées de f avec elle même.
Les erreurs de calculs propres à l'approximation
décimale
tronquée d'un réel dans scilab conduisent
à des
phénomènes abérents : en prenant
x=1.61, on
devrait obtenir une erreur de division par 0 après 9
itérations de f (les itérés de f ne
sont
définis qu'en dehors des nombres rationnels). Or on obtient
un
phénomène périodique stable de
période 4.
Sauf erreur de ma part le système dynamique
associé
à f n'a pas d'orbite périodique stable.
En fait l'erreur dans le calcul de f(x) est multipliée par
x*f(x) (>2) lors de chaque itération. Les valeurs
trouvées
après itérations n'ont très vite
aucune pertinence.
-->//Calcul
de valeurs propres et de vecteurs propres
-->
A=[1,1;1,0];[D,P]=bdiag(A)
P
=
0.8506508 - 0.5257311
0.5257311 0.8506508
D
=
1.618034 0.
0.
- 0.6180340
--> A*P(:,1)-D(1,1)*P(:,1) //verification
ans =
0.
0.
-->//points fixes des sections de f
--> x=[];for i=1:10;a=spec([i,1;1,0]);x(i)=a(2);end;x
x =
1.618034
2.4142136
3.3027756
4.236068
5.1925824
6.1622777
7.1400549
8.1231056
9.1097722
10.09902
--> (1+sqrt(5))/2
ans =
1.618034
-->1/(sqrt(2)-1)
ans =
2.4142136
--> function y=f(x);y=1/(x-int(x));endfunction
-->//
Comportement des iteres de f au voisinage du premier point fixe
-->
y=[];y(1)=(1+sqrt(5))/2;for i=1:1000;y(i+1)=f(y(i));end;
--> clf();plot2d(1:1000,y(1:1000).^(-1),0)
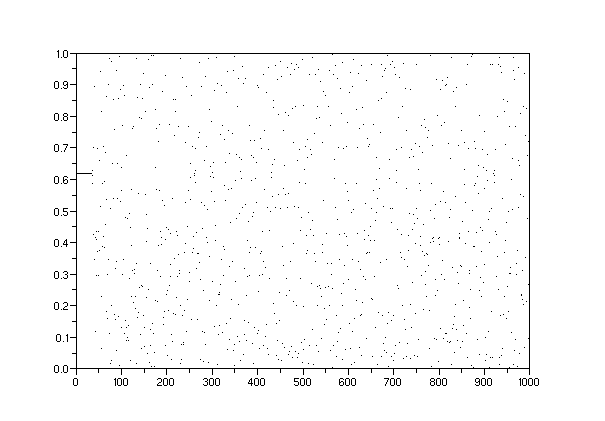
-->// Points de periode 2
-->[D,P]=bdiag([1,1;1,0]*[2,1;1,0])
P =
0.8068982 - 0.3577590
0.5906905
0.9774159
D =
3.7320508
0.
0.
0.2679492
-->a=P(1,1)/P(2,1)
a =
1.3660254
-->function []=dessin(a,n);y=[];y(1)=a;for i=1:n-1;y(i+1)=f(y(i));end;plot2d(1:n,y(1:n).^(-1),0);endfunction
-->clf();dessin(a,100)
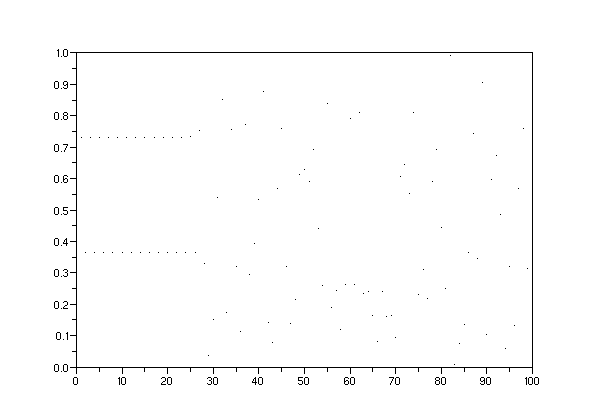
-->//Rq sur le spectre :
-->a=bdiag([5,1;1,0]*[3,1;1,0]*[4,1;1,0])
a =
72.013886
0.
0.
- 0.0138862
-->x=[];for i=1:100;a=spec([i,1;1,0]);x(i)=a(2);end;
-->x(find(x>72,1))
ans =
72.013886
-->a(1,1)-x(find(x>72,1))
ans =
1.421D-14
-->// Les iteres de f ne sont pas definis sur les nombres
rationnels :
-->function i=g(a,b);i=1;while
b<>0;r=a-int(a/b)*b;a=b;b=r;i=i+1;end;endfunction
-->g(1618034,1000000) //nbre d'iterations pour une division par
zero si les calculs etaient exacts
ans =
23.
-->2*log(1618034)/log(2)
ans =
41.251621
-->clf();dessin(1.618034,24)
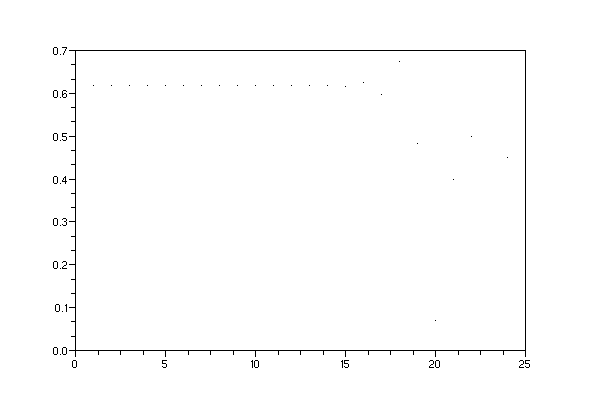
-->clf();dessin(1.6,24) //essai
avec un nbre rationnel plus proche d'un entier
!--error 27
division by zero...
at line 2
of function f called by :
line 2 of function dessin called by :
clf();dessin(1.6,24)
-->g(16,10)
ans =
5.
-->g(161,100)
ans =
9.
-->clf();dessin(1.61,100) //Y aura
t-il une erreur de division par 0 ?
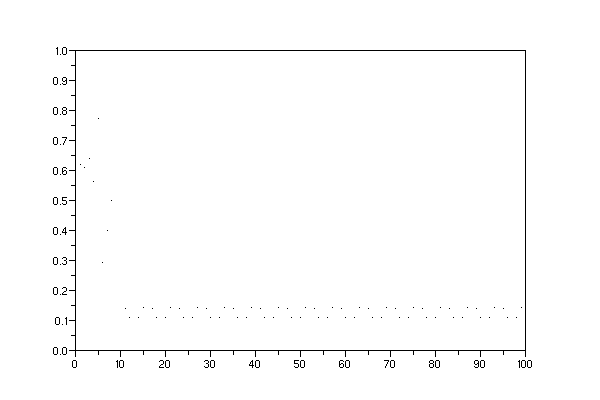
-->clf();dessin(1.61,10000)
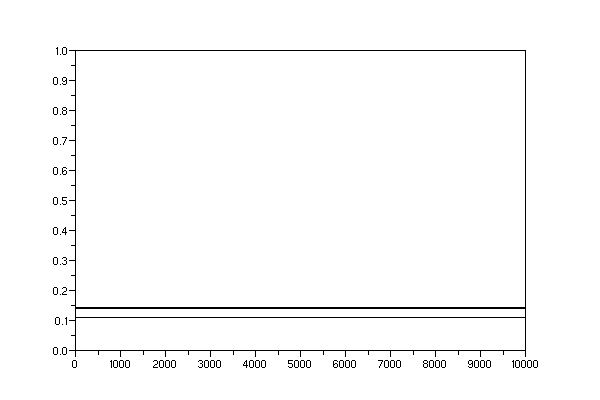
-->// Controle de la precision dans l'approximation decimale
d'un reel par Scilab
-->number_properties("radix")
ans =
2.
-->number_properties("digits")
ans =
53.
-->a=(1+sqrt(5))/2;log(a-f(a))/log(2)
ans =
- 52.
-->b=2*log(a)/log(2) //nbre theorique de chiffres significatifs
perdus sur les 53 (en base 2) lors de chaque iteration
b =
1.38848382726123476
-->53/b //nbre theorique d'iterations avant une erreur de
l'ordre de grandeur de a
ans =
38.1711323959327444
-->clf();dessin(a,40)
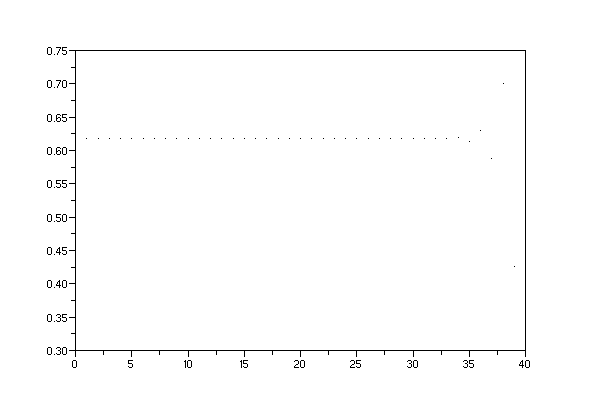
-->log(abs(y(37)-a))/log(2) //ecart avec a après 36
iterations
ans =
- 3.58964805665926656
-->53-36*b //ecart theorique
ans =
3.01458221859554953
-->// intervalle de confiance - on approxime f([a-eps,a+eps])
par [f(a-eps),f(a+eps)] valable si [a-eps,a+eps] est inclu dans
un intervalle ]k,k+1[. Si ]a-eps,a+eps[ contient un entier alors f(]a-eps,a+eps[) est ]1,+infty[
-->// Troncature decimale vecue :
-->a=(1+sqrt(5))/2;[(a+2^(-53))-a,(a+2^(-52))-a]
ans =
0.
2.220D-16
-->function
[]=dessin(a,n);y1(1)=a-2^(-52);y2(1)=a+2^(-52);for
i=1:n-1;y1(i+1)=f(y1(i));y2(i+1)=f(y2(i));end;
xset("color",color(230,230,230));for
i=1:10;xfrect(0,1/(2*i),40,1/(2*i*(2*i+1)));end;for
i=1:n;plot2d([i,i],[1/y1(i),1/y2(i)],style=1);end;endfunction
Warning :redefining function: dessin
-->clf();dessin((1+sqrt(5))/2,40) // a comparer avec la derniere
figure ci-dessus :

-->clf();dessin(1.61,40) //a comparer avec le phenomene de periodicite
observe plus haut :
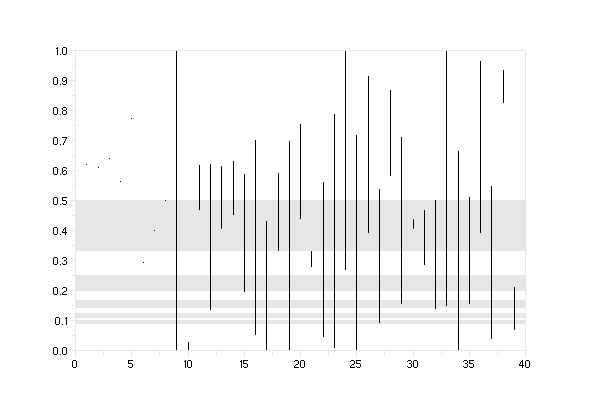
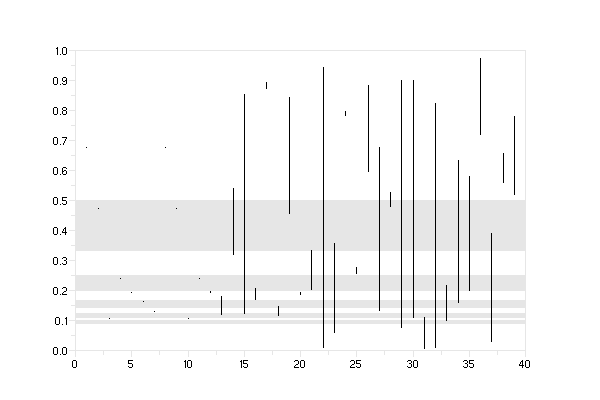
-->//Points
de periode 7 ?
-->[D,P]=bdiag([1,1;1,0]*[2,1;1,0]*[9,1;1,0]*[4,1;1,0]*[5,1;1,0]*[6,1;1,0]*[7,1;1,0]);clf();dessin(P(1,1)/P(2,1),40)
fx dehon,
24 janvier 2008








