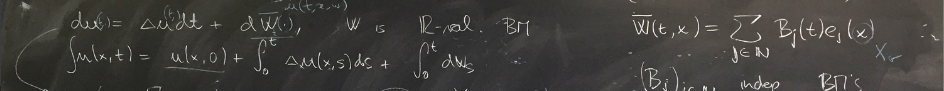ERC ELISA Online Probability Seminar

• Speaker: André Galligo, Université Côte d'Azur


• Title: Principes de grandes déviations et dynamique asymptotique de nuages de racines de polynômes dérivés.


• Abstract: On remarque d'abord que la dérivée (N-k)ième d'un polynôme P de degré N est proportionnelle à la moyenne des polynômes caractéristiques des k x k mineurs principaux des matrices S D S^(-1), où D est la matrice diagonale construite avec les racines de P et S parcourt les matrices de permutation. Je commencerai par un rappel sur les LDP et des théorèmes de J. Trashorras sur les LDP de mesures empiriques symetrisées (2008). Puis, je présenterai la stratégie de la très récente approche variationnelle de Arizmendi et Johnston (arXiv Septembre 2023). Elle re-interprète de nombreux résultats sur les évolutions de spectres réels de matrices aléatoires en remplaçant les moyennes sous l'action du groupe unitaire par des moyennes sous l'action du groupe symétrique. Ainsi, en notant \mu la mesure limite des mesures empiriques des racines d'une famille de polynômes P_N et (avec 0<\tau<1), [\mu]_\tau la mesure limite des mesures empiriques des racines de la derivee [(1-\tau) N]ième de P_N , on obtient la relation suivante qui détermine l'évolution de [\mu]_\tau : \int_{\R} log(z-\lambda) [\mu]_\tau d\lambda = 1/\tau int_{\R} log(\omega-\lambda) [\mu] d\lambda +log(\tau)-\frac{1-\tau}{\tau} log (\frac{\omega-z}{1-\tau}) ; où \omega est une fonction de z et \tau déduite de la transformée de Cauchy de \mu . Une relation que nous aimerions généraliser d'une part aux polynômes avec des racines complexes, d'autre part en remplaçant la derivation par une certaine opération "voisine" comportant un aléa qui s'uniformise quand N tend vers l'infini.


• Zoom link: Meeting ID : 899 5693 1785 Code : 260168


• Room: Fizeau

• Speaker: Giacomo Sodini, University of Vienna


• Title: Dissipative evolutions in the space of probability measures


• Abstract: We introduce a notion of multivalued dissipative operator (called Multivalued Probability Vector Field - MPVF) in the 2-Wasserstein space of Borel probability measures on a (possibly infinite dimensional) separable Hilbert space. Taking inspiration from the theories of dissipative operators in Hilbert spaces and of Wasserstein gradient flows, we study the well-posedness for evolutions driven by such MPVFs, and we characterize them by a suitable Evolution Variational Inequality (EVI). Our approach to prove the existence of such EVI-solutions is twofold: on one side, under an abstract stability condition, we build a measure-theoretic version of the Explicit Euler scheme showing novel convergence results with optimal error estimates; on the other hand, under a suitable discrete approximation assumption on the MPVF, we recast the EVI-solution as the evolving law of the solution trajectory of an appropriate dissipative evolution in an L^2 space of random variables. This talk is based on a joint work with Giulia Cavagnari and Giuseppe Savaré.

• Speaker: Gonçalo Dos Reis, University of Edinburgh


• Title: High order splitting methods for stochastic differential equations


• Abstract: In this talk, we will discuss how ideas from rough path theory can be leveraged to develop high order numerical methods for SDEs. To motivate our approach, we consider what happens when the Brownian motion driving an SDE is replaced by a piecewise linear path. We show that this procedure transforms the SDE into a sequence of ODEs – which can then be discretized using an appropriate ODE solver. Moreover, to achieve a high accuracy, we construct these piecewise linear paths to match certain “iterated” integrals of the Brownian motion. At the same time, the ODE sequences obtained from this path-based approach can be interpreted as a splitting method, which neatly connects our work to the existing literature. For example, we show that the well-known Strang splitting falls under this framework and can be modified to give an improved convergence rate. We will conclude the talk with a couple of examples, demonstrating the flexibility and convergence properties of our methodology.
  (Joint work with James Foster and Calum Strange, arXiv version)

• Speaker: Alpar Meszaros, Durham University


• Title: Mean field games and master equations trough the lens of conservation laws


• Abstract: In this talk we present a new nonlinear transport equation written on the space of probability measures that allows to study mean field games and master equations. We will consider deterministic problems. The point of view via this transport equation has two important consequences. First, this equation reveals a new monotonicity condition which is sufficient both for the uniqueness of MFG Nash equilibria and for the global in time well-posedness of master equations. Interestingly, this condition is in general in dichotomy with both the Lasry--Lions and displacement monotonicity conditions, studied so far in the literature. Second, in the absence of monotonicity, the conservative form of the transport equation can be used to define weak entropy solutions to the master equation. We construct several concrete examples to demonstrate that MFG Nash equilibria, whether or not they actually exist, may not be selected by the entropy solutions of the master equation.
  The talk will be based on joint works with J. Graber (Baylor University).

• Speaker: Alekos Cecchin, Padoue


• Title: On the long time behavior of mean field control problems


• Abstract: We study the long time behavior of controlled McKean-Vlasov dynamics with a non-degenerate idiosyncratic noise, without assuming convexity, nor monotonicity, of the cost coefficients. Instead, we consider a drift component which is strongly decreasing, but just outside a ball. Using coupling by reflection arguments, we establish uniform in time estimates for the Lipschitz constant of the value function of the mean field control problem and of its measure derivative. Thus we show existence and uniqueness of the turnpike, i.e. the stationary measure which solves the ergodic problem, and establish exponential convergence of the optimal trajectories to such equilibrium, as the time horizon grows. We also prove uniform in time propagation of chaos for the related symmetric control problem with N cooperative agents.
  Based on joint work with Giovanni Conforti, Alain Durmus, and Katharina Eichinger (Ecole Polytechnique).

• Speaker: Ludovic Tangpi, Princeton


• Title: A probabilistic approach to vanishing viscosity for PDEs on the Wasserstein space


• Abstract: In this talk we present an analogue, for partial differential equations on the space of probability measures, of the classical vanishing viscosity result known for equations on the Euclidean space. Our result allows in particular to show that the value function arising in various problems of classical mechanics and games can be obtained as the limiting case of second order PDEs. The method of proof builds on stochastic analysis arguments and allows for instance to prove a Freindlin-Wentzell large deviation theorem for McKean-Vlasov equations.

• Speaker: Thomas Leblé, CNRS, Université Paris Descartes


• Title: Rigidité(s) du gaz de Coulomb 2d (& friends)


• Abstract: Le gaz de Coulomb (ou "one-component plasma", ou "log-gas") est un système de physique statistique présentant des liens plus ou moins accidentels avec certains modèles de matrices aléatoires, des problèmes type "configurations optimales de points", l'effet Hall quantique etc. La littérature physique lui prédit une transition liquide/solide qui reste totalement incomprise du point de vue mathématique. Numériquement, on observe un passage d'une structure quasi-cristalline (à basse température) à quelque chose de pseudo-Poissonnien (à haute température). Néanmoins, on sait démontrer que le système conserve un certain caractère ordonné à toute température. Je mentionnerai à ce sujet :
  1) Des bornes optimales sur la variance de statistiques lisses.
  2) Une borne (non-optimale) sur la variance du nombre de points, qui implique que le gaz a la propriété remarquable d'être "hyperuniforme".
  3) Un résultat amusant de "rigidité de nombre" pour le système infini.
  4) Des contrôles sur les distances de Wasserstein entre la mesure empirique des particules et la densité uniforme, qui rangent le système du côté "ordonné" et non du côté "iid".
  Travaux avec S. Serfaty, T. Vasseur et R. Lachièze-Rey.

• Speaker: Samuel Daudin, Université Côte d'Azur


• Title: On the optimal rate for the convergence problem in mean-field control


• Abstract: In this talk I will present a recent joint work with François Delarue and Joe Jackson about the convergence problem in mean-field control theory. The goal is to obtain optimal rates for the convergence of the value functions associated to the different problems, in general situations where no structural condition (convexity, displacement convexity) ensures the uniqueness and stability of optimal solutions for the limiting problem. In particular we don’t expect propagation of chaos for the particle system and the value function associated to the limiting problem might not be differentiable. Our main result is to derive sharp rates of convergence in two distinct regimes. When the data is sufficiently regular we obtain rates proportional to N^(-1/2), N being the number of particles. When the data is merely Lipschitz and semi-concave with respect to the first Wasserstein distance we obtain rates proportional to N^{-2/3d}, close to the optimal rates for uncontrolled particle systems. Although one inequality between the value functions follows by classical control theoretic argument, the other one proves more difficult. Our strategy consists then in several mollifying arguments to produce approximations of the value function for the mean-field problem which are almost classical sub-solutions to the dynamic programming equation and conclude by a comparison argument. We also provide some examples to show that our results are sharp.

• Speaker: Joe Jackson, University of Texas at Austin


• Title: Approximately optimal distributed stochastic controls beyond the mean field setting


• Abstract: In this talk I will present a recent joint work with Daniel Lacker, in which we study a class of high-dimensional stochastic optimal control problems. We consider both the full-information problem, in which each agent observes the states of all other agents, and the distributed problem, in which each agent observes only its own state. Our main results are sharp non-asymptotic bounds on the gap between these two problems, measured both in terms of their value functions and optimal states. Along the way, we develop theory for distributed optimal stochastic control in parallel with the classical setting, by characterizing optimizers in terms of an associated stochastic maximum principle and a Hamilton-Jacobi-type equation. Our original motivation for this project comes from mean field control, and by specializing our results to the mean field setting we obtain the optimal rate of convergence for displacement convex data. We also apply our results to a control problem with "heterogeneous doubly stochastic interactions" and derive conditions under which the usual mean field limit is a good approximation, despite the asymmetry in the model.

• Speaker: Pierre Lavigne, Institut Bachelier (Paris)


• Title: Decarbonization of financial markets: a mean field game approach


• Abstract: We present a model of a financial market where a large number of firms determine their dynamic emission strategies under climate transition risk in the presence of both green-minded and neutral investors. The firms aim to achieve a trade-off between financial and environmental performance, while interacting through the stochastic discount factor, determined in equilibrium by the investors’ allocations. We formalize the problem in the setting of mean-field games and prove the existence and uniqueness of a Nash equilibrium for firms. We then present a convergent numerical algorithm for computing this equilibrium and illustrate the impact of climate transition risk and the presence of green-minded investors on the market decarbonization dynamics and share prices. We show that uncertainty about future climate risks and policies leads to higher overall emissions and higher spreads between share prices of green and brown companies. This effect is partially reversed in the presence of environmentally concerned investors, whose impact on the cost of capital spurs companies to reduce emissions.. Joint work with Peter Tankov. See arXiv submission.

• Speaker: Khoa Lê, Leeds (UK)


• Title: McKean--Vlasov equations with rough common noise and quenched propagation of chaos


• Abstract: We show well-posedness and propagation of chaos for McKean–Vlasov equations with rough common noise and progressively measurable coefficients. Our results are valid under minimal regularity assumptions on the coefficients, in agreement with the respective requirements of Itô and rough path theory. To achieve these goals, we work in framework of rough stochastic differential equations. Joint work with Peter Friz and Antoine Hocquet