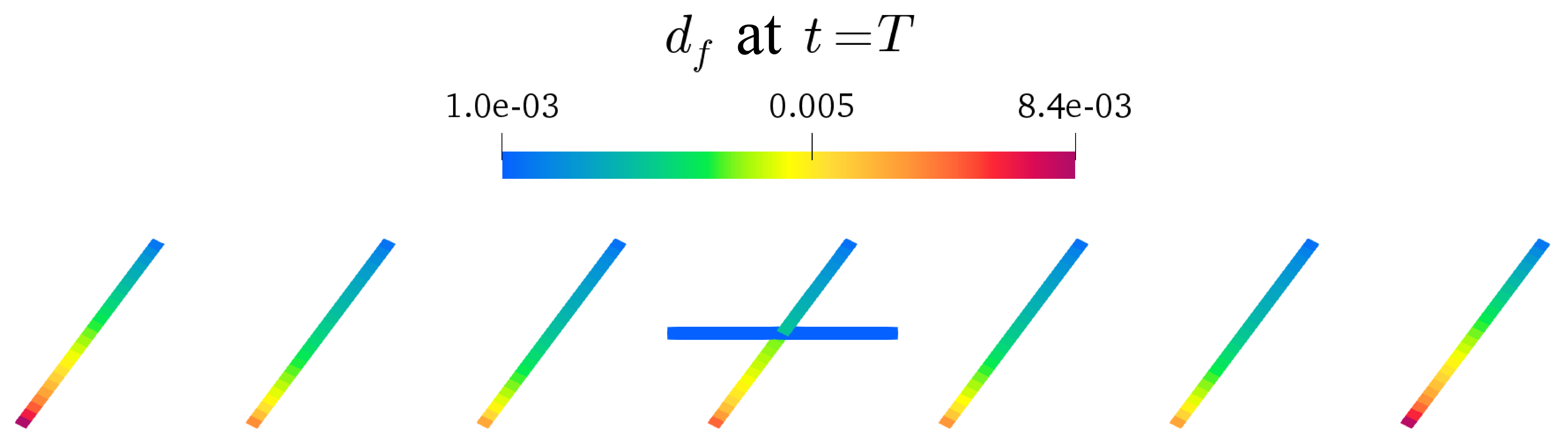Normal faults in volcanic ashes and paleo-soils, El Salvador, photo by Chuck DeMets
HDTHM associate team
Mathematical and numerical methods for thermo-hydro-mechanical models in porous media with discontinuities
- Teams: the project is a collaboration between:
- Members of Inria-LJAD team Coffee involved in the project:
Roland Masson (PI):
- Professor at the department of Mathematics J.A. Dieudonné, University Nice Sophia Antipolis.
- Member of the joint Inria-LJAD team Coffee.
- Domain of expertise: finite volume discretization of PDEs, discretization of multiphase Darcy flows in heterogeneous and fractured porous media, formulation and discretization of multiphase compositional Darcy flows, multi-physics coupling algorithms and domain decomposition methods, applications to reservoir, basin, geothermal systems, and geological storage modelling.
Konstantin Brenner:
- MCF at the department of Mathematics J.A. Dieudonné, University Nice Sophia Antipolis.
- Member of the joint Inria-LJAD team Coffee.
- Domain of expertise: finite volume discretization of PDEs, convergence of numerical schemes, modeling and discretization of multi-phase Darcy flow with strong capillary pressure heterogeneities, accelerated Newton's method for nonlinear PDEs.
Laurent Monasse :
- CR at Inria-Sophia Antipolis Méditerranée.
- Member of the joint Inria-LJAD team Coffee.
- Domain of expertise: finite volume discretization of PDEs,
fluid-structure interaction, solid mechanics, fracture dynamics,
Discrete Element methods.
El Houssaine Quenjel :
- Postdoctoral researcher at the department of Mathematics J.A. Dieudonné, University Nice Sophia Antipolis in 2019-2020. Funded by the ANR project CHARMS.
- Member of the joint Inria-LJAD team Coffee in 2019-2020.
- Domain of expertise: discretization and numerical analysis for compressible gas liquid Darcy flows in porous media, positive finite volume schemes for nonlinear degenerate parabolic equations and two phase Darcy flows.
Francesco Bonaldi :
- Postdoctoral researcher in the joint Inria-LJAD team Coffee in 2019-2021, University Côte d'Azur, Inria, CNRS, LJAD in collaboration with laurent Trenty from Andra. Funded by Andra.
- Member of the joint Inria-LJAD team Coffee in 2019-2021.
- Domain of expertise: Nonconforming high-order numerical methods, PDEs, Multiphysics problems, Mechanics of thin structures, Asymptotic methods.
- Members of the School of Mathematical Sciences, Monash University involved in the project:
Jérome Droniou (co-PI) :
- Associate Professor in the School of Mathematical Sciences, Monash University, Australia
- Domain of expertise: finite volume and hybrid high-order methods for linear and non-linear models, convergence analysis of schemes for non-linear and coupled models -- including multiphasic flows in fractured networks, discretisation and analysis of advection-dominated models, theoretical analysis of partial differential equations and its discrete translations to numerical schemes.
Kim-Ngan Le :
- PostDoc researcher in the School of Mathematical Sciences, Monash University, Australia. Funded by the Australian Research Council (Discovery Project number DP170100605; lead CI: A/Prof. J. Droniou), 01/12/17--31/12/19 with options for extension.
- Domain of expertise: theoretical and numerical analysis of stochastic partial differential equations, numerical methods for miscible porous media flows, characteristic methods for advection models.
Context of the HDTHM project:
Many real life applications in the geosciences involve processes like multi-phase, non-isothermal flow or hydro-mechanical coupling in heterogeneous porous media. Such mathematical models are commonly coupled systems of partial differential equations, including nonlinear and possibly degenerate parabolic ones. Next to the inherent difficulties posed by such equations, further challenges are due to the heterogeneity of the medium and the presence of discontinuities like fractures. This has a strong impact on the complexity of the models, challenging their mathematical and numerical analysis and the development of efficient simulation tools.
This collaboration focuses on the so called hybrid-dimensional matrix fracture models obtained by averaging both the unknowns and the equations in the fracture width and by imposing appropriate transmission conditions at both sides of the matrix fracture interfaces. Given the high geometrical complexity of real life fracture networks, the main advantages of these hybrid-dimensional compared with full-dimensional models are to both facilitate the mesh generation and the discretisation of the model, and to reduce the computational cost of the resulting schemes. This type of hybrid-dimensional models is the object of intensive researches since the last 15 years due to the ubiquity of fractures in geology and their considerable impact on the flow and transport of mass and energy in porous media, and on the mechanical behavior of the rocks.
Objectives of the HDTHM project: Hybrid-dimensional matrix fracture models combine geometrical complexity with highly contrasted properties and constitutive laws at the matrix fracture interfaces leading to strong nonlinear couplings and a large range of space and time scales. It leads to new challenges in terms of mathematical analysis, discretization, nonlinear solvers and preconditioners.
Building up on our successful collaboration on hybrid-dimensional two-phase flow models, the objective of this project is to design novel numerical methods for two classes of hybrid-dimensional matrix fracture models, motivated by applications to geothermal systems.
On the one hand, we will focus on thermo-hydro models with nonlinear coupling of the porous media variable density flow with the energy conservation equation.
On the other hand, we will consider hydro-mechanical models that
couple the hybrid-dimensional porous media flow with the mechanical
deformation of the matrix. For such models, the flow in the
fractures has a strong nonlinear dependence upon the fracture width,
resulting from the matrix mechanical deformation which itself depends
on the fluid pressure in the fractures.
Visits:
- Jérome Droniou, El Houssaine Quenjel, Konstantin Brenner and Roland Masson participated to the workshop POEMS 29th april - 3rd may 2019 on POlytopal Element Methods in Mathematics and Engineering.
- Visit of Konstantin Brenner and Roland Masson at Monash University for one month in july 2019 to collaborate with Jérome Droniou on two-phase Darcy flows in deformable fractured porous medium.
- Visit of El Houssaine Quenjel at Monash University for one month in november 2019: ongoing collaboration on the total velocity formulations of two-phase Darcy flows in heterogeneous porous media with different rocktypes.
- Visit of Jérome Droniou at University Côte d'Azur as visiting professor for one month in june-july 2020, reported to 2022 due to covid crisis
- Konstantin Brenner was plenary speaker at the CTAC2020 conference, Sydney, Australia 30-Aug to 2nd-Sep 2020.
- Visit of Jérome Droniou at University Côte d'Azur as visiting professor for 3 months in september-november 2022.
Achievements:
- During the one month visit to Monash we have jointly investigated gradient discretizations of two phase Darcy flows in fractured and deformable porous medium and established their convergence to a weak solution using compacity arguments. The models are hybrid-dimensional in the sense that fractures are represented as co-dimension one surfaces coupled with the surrounding matrix domain by transmission conditions. Our first work deals with open fractures combined with the continuous pressure transmission condition assuming that both phase pressures are continuous at matrix fracture interfaces [3]. This is the first result of convergence for such models, since previous analysis were restricted to linear and single phase fractured poro-mechanical models.
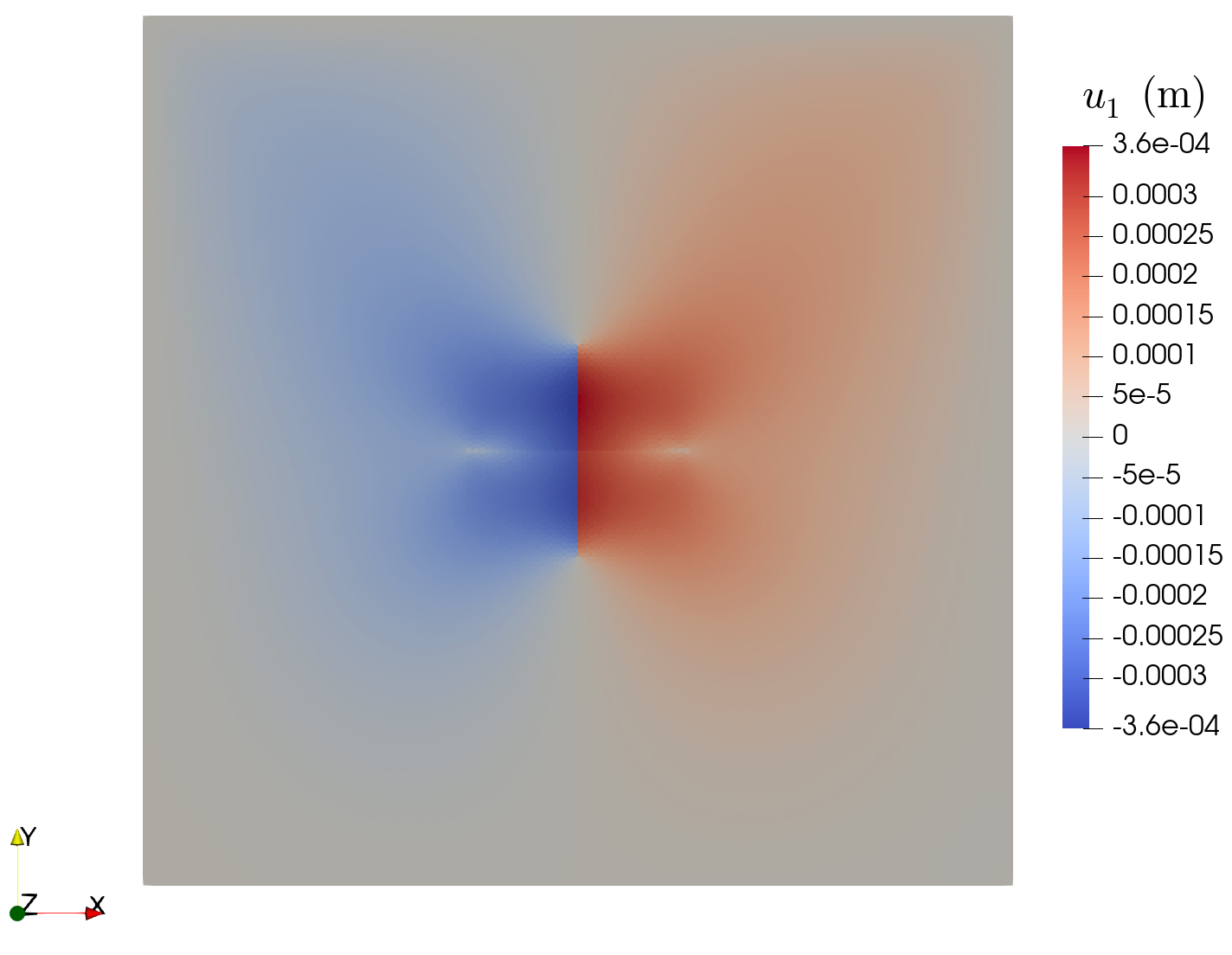
- Gas injection in two cross shaped fractures using the continuous pressure model
- Porous medium initially water saturated
- Injection of gas in the fractures
- 2D triangular mesh of 230 000 cells of the domain (0,100)x(0,100)
- TPFA scheme for the DFM two-phase flow model coupled with P2 FE for the mechanics
- Gas saturation and displacement fields (in m) in the x and y directions at final time


Our analysis is extended in [6] to the case of discontinuous pressure models based on nonlinear transmission conditions at matrix fracture interfaces. As opposed to continuous pressure models, this type of model can account for the discontinuity of one phase pressure induced at matrix fracture interfaces by its low fracture relative permeability which can arise when the fracture is almost fully filled by the other phase. This model is applied to simulate the desaturation by suction of a Callovo-Oxfordian (COX) argilite storage rock in the fractured Excavation Damaged Zone (EDZ) with data set provided by Andra.
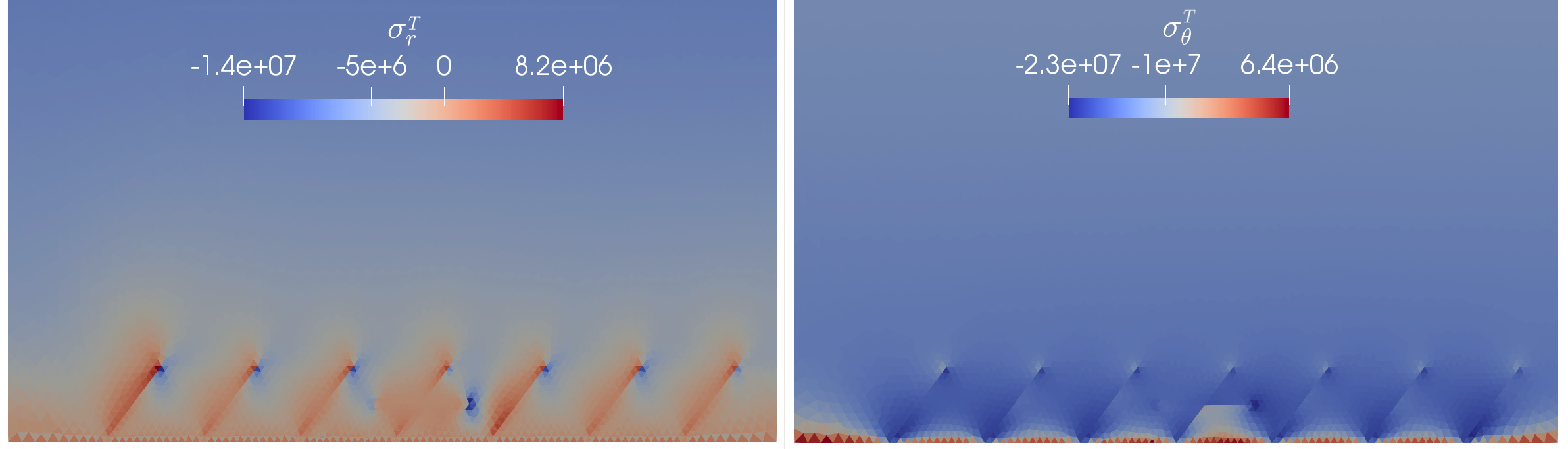
- Desaturation by suction of the fractured EDZ: comparison between the continuous and discontinuous pressure models
- Porous medium initially water saturated
- Atmospheric gas pressure and fixed gas saturation at the bottom boundary
- Axi-symmetric model with a 2D triangular mesh of 28945 cells of the x-r domain (0,10)x(5,35)
- Fracture network in the EDZ: 7 oblique fractures and 1 horizontal fracture
- TPFA scheme for the DFM two-phase flow model coupled with P2 FE for the mechanics
- Gas saturation at final time for the discontinuous (left) and continuous (right) pressure models
- Radial and orthoradial total stresses for the discontinuous pressure model

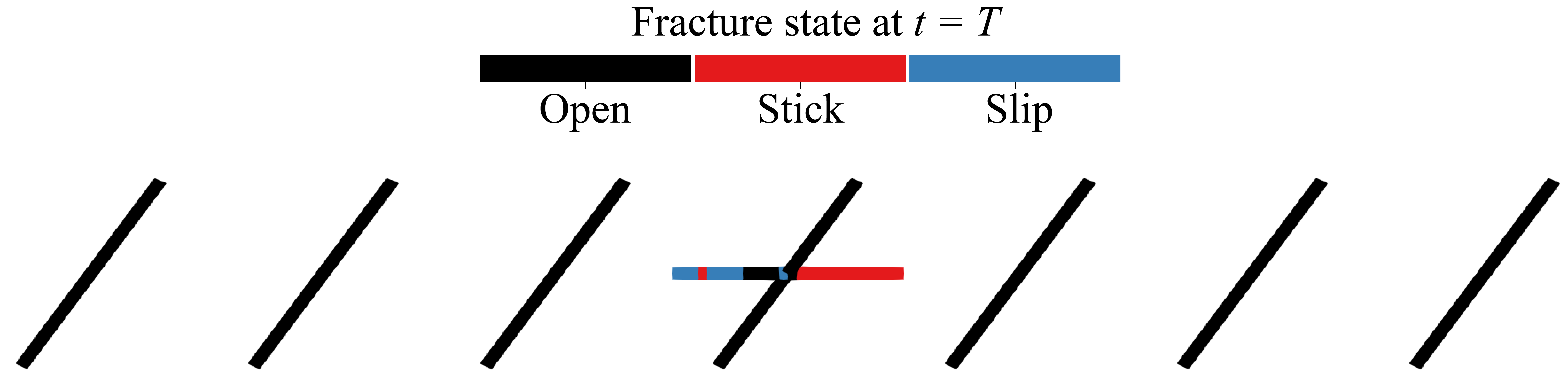
The model is extended in [7] to account for Coulomb frictional contact at matrix-fracture interfaces. The discretization is based on a mixed formulation using face-wise constant Lagrange Multipliers and P2 Finite Element for the displacement field. We prove the stability of the discrete model in energy norm as well as the existence of the discrete solution. The contact-mechanical model is first validated on analytical and reference solutions, then used to simulate desaturation by suction of the fractured EDZ.
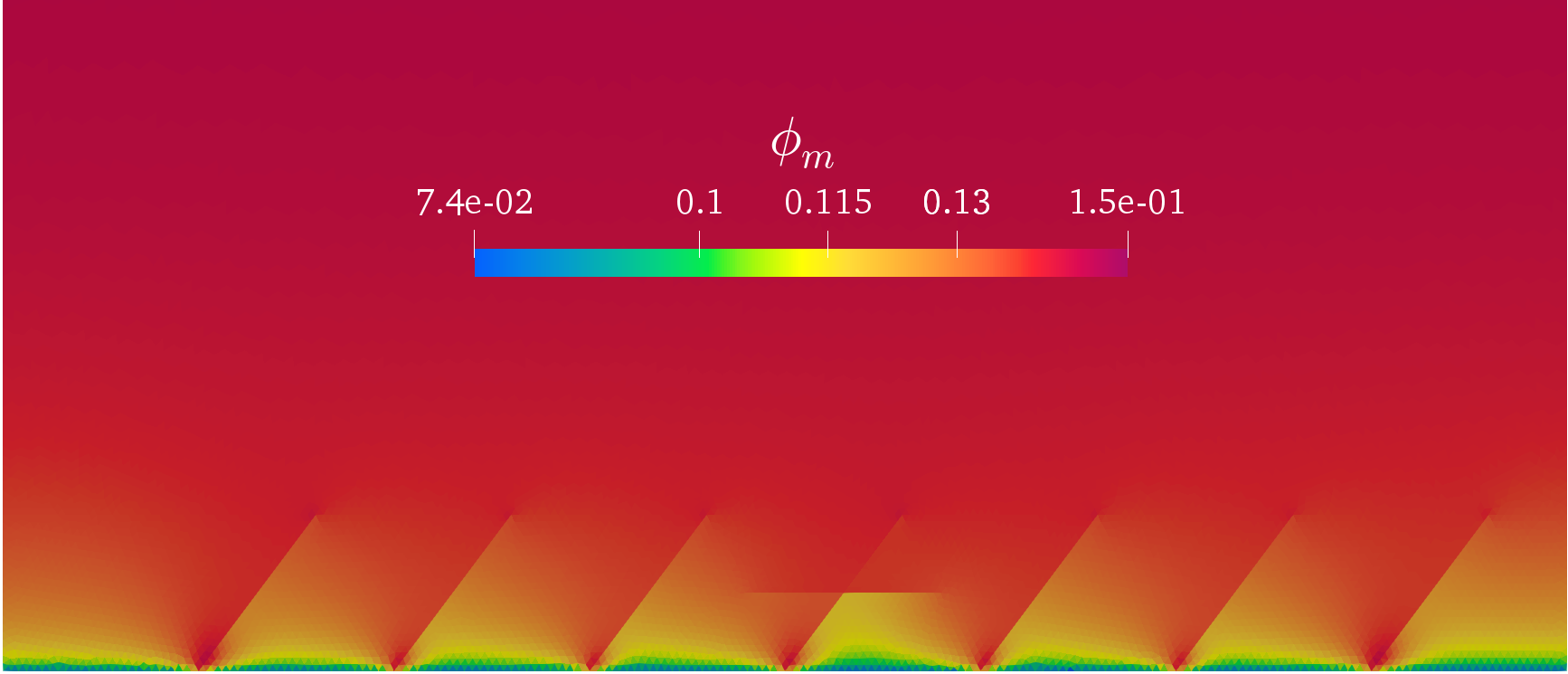
- Desaturation by suction of the fractured EDZ: discontinuous pressure model with Coulomb frictional contact at matrix-fracture interfaces
- Same data set as above with friction coefficient F=0.5 and fracture aperture at contact state d0=1 mm.
- Contact state (open-stick-slip) and fracture aperture at final time along the fractures. Matrix porosity at final time.
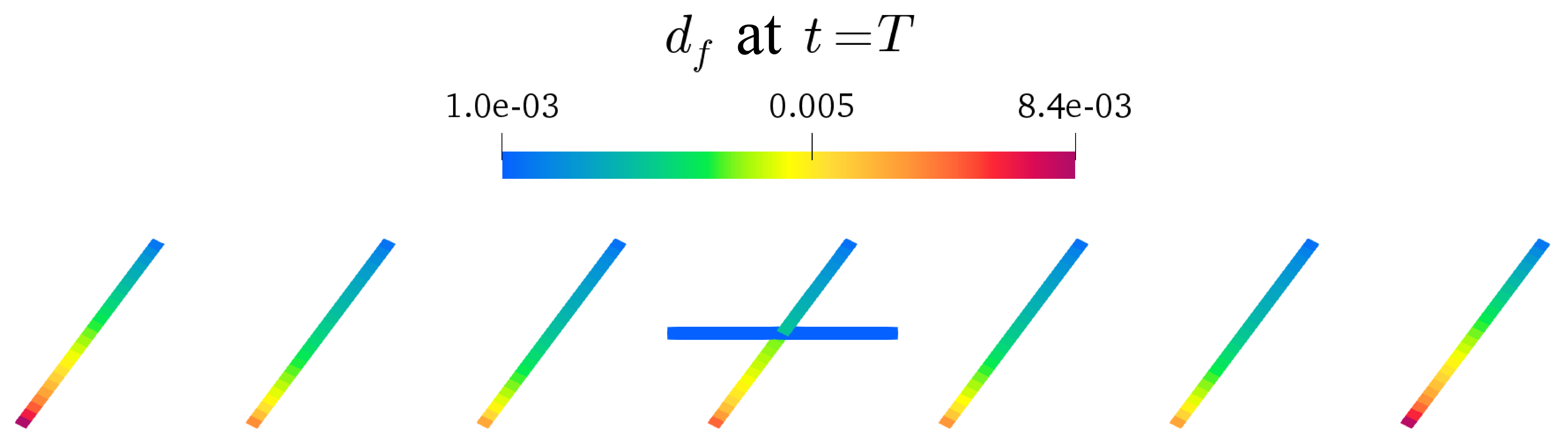
We investigate in [5] a finite volume scheme for two-phase Darcy flow in heterogeneous porous media with different rock types. The discretization is based on cell centered as well as face centered degrees of freedom in order to capture accurately the nonlinear transmission conditions at different rock type interfaces. These conditions play a major role in the flow dynamics. The scheme is formulated with natural physical unknowns avoiding the cumbersome use of the global pressure. It combines a Two-Point Flux Approximation of the gradient normal fluxes with a Hybrid Upwinding approximation of the transport terms. The convergence of the scheme to a weak solution is established taking into account discontinuous capillary pressure at different rock type interfaces and the degeneracy of the phase mobilities.
In [8]
we carry out a convergence analysis of a discrete mixed-dimensional single phase poromechanical model using compactness arguments.
The model we consider has a range of challenging features: frictionless contact at matrix--fracture interfaces, complex fracture networks, nonlinear dependence of the flow on the fracture aperture, as well as the degeneracy of the fracture conductivity at the fracture tips. The analysis we carry out moreover covers many different numerical approximations of the flow and mechanical components of the model. As a by-product of this convergence analysis, we also obtain the existence of a weak solution to the continuous model.
To the best of our knowledge, this is the first complete numerical analysis of such a complex poromechanical model, with all the above-mentioned features.
Fundings:
- Monash University has funded the visit of Roland Masson at the School of Mathematics in july 2019
- Andra is funding the project "Numerical modelling of coupled liquid gas Darcy flow and mechanical deformation in fractured porous media" covering the postdoctoral fellowship of Francesco Bonaldi for two years started in september 2019.
- Jérome Droniou has obtained a visiting professor position at University Côte d'Azur for 3 months in 2022
- Andra and BRGM are funding the PhD of Mohamed Laaziri started in december 2022 dealing with "Numerical modelling of coupled non-isothermal Darcy flow and mechanical deformation in fractured porous media"
- The postdoctoral fellowship of Ali Haidar started in january 2023 is funded by the Inria/IFPEN partnership. It deals with Non matching discretizations of mixed- dimensional poromechanical modesl with frictionless contact at matrix fault interfaces, application to fault reactivation assessment in CO2 storages
Joint publications:
- [1] Numerical Analysis of a Two-Phase Flow Discrete Fracture Model J. Droniou, J. Hennicker, R. Masson, Numerische Mathematik, january 2019, volume 141, issue 1, pp 21-62.
- [2] The Gradient Discretisation Method for Two-phase Discrete Fracture Matrix Models in Deformable Porous Media F. Bonaldi, K. Brenner, J. Droniou, R. Masson FVCA 2020 - International Conference on Finite Volumes for Complex Applications IX, Jun 2020, Bergen, Norway. Springer , June 2020.
- [3]
Gradient discretization of two-phase flows coupled with mechanical deformation in fractured porous media F. Bonaldi, K. Brenner, J. Droniou, R. Masson, Computers and Mathematics with Applications; 98, pp 40-68, 2021.
- [4] Two-Phase Darcy Flows in Fractured and Deformable Porous Media, Convergence Analysis and Iterative Coupling, F. Bonaldi, K. Brenner, J. Droniou, R. Masson, Conference Proceedings, ECMOR XVII, 1-20, DOI:10.3997/2214-4609.202035013 , september 2020.
- [5] Total-velocity-based finite volume discretization of two-phase Darcy flow in highly heterogeneous media with discontinuous capillary pressure K. Brenner, J. Droniou R. Masson, E.H. Quenjel, IMA Jounal of Numerical Analysis, avril 2021.
- [6]
Gradient discretization of two-phase poro-mechanical models with discontinuous pressures at matrix fracture interfaces F. Bonaldi, K. Brenner, J. Droniou, R. Masson, A. Pasteau, L. Trenty, ESAIM: Mathematical Modelling and Numerical Analysis, accepted july 2021.
- [7]
Energy stable discretization of two-phase flow in deformable porous media with frictional contact at matrix-fracture interfaces F. Bonaldi, J. Droniou, R. Masson, A. Pasteau, Journal of Computational Physics accepted january 2022.
- [8]
Numerical analysis of a mixed-dimensional poromechanical model with frictionless contact at matrix-fracture interfaces
F. Bonaldi, J. Droniou, R. Masson, january 2022.
Updated 03-02-2022