Fabrication additive

La méthode de déshomogénisation appliquée au cas tridimensionnel permet d'optimiser des pièces élastiques formées de micro-structures exploitant ainsi le potentiel des procédés de fabrication additive.
Déshomogénéisation
Une suite de formes convergeant vers le composite optimal est obtenue comme post-traitement de la méthode d'homogénéisation. Cette méthode a été appliquée à des composites optimaux localement périodiques difféomorphes à un réseau structuré.
Optimisation Hybride
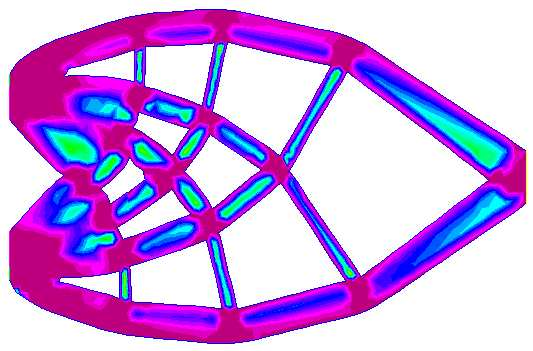
L'optimisation de forme hybride combine les méthodes d'optimisation topologique, géométrique et d'homogénéisation. L'idée consiste à passer progressivement de méthode d'homogénéisation classique à la méthode géométrique/topologique.
Sauts de conductivité
L'utilisation naïve de la méthode de dérivation rapide de Céa conduit à une version erronée de la dérivée de forme. La dérivée de forme géométrique peut être obtenue comme limite de la dérivée de forme paramétrique classique.
Activation des axones

Quelle est l'influence du positionnement d'une électrode bipolaire sur l'activation des axones ?
Globules Rouges
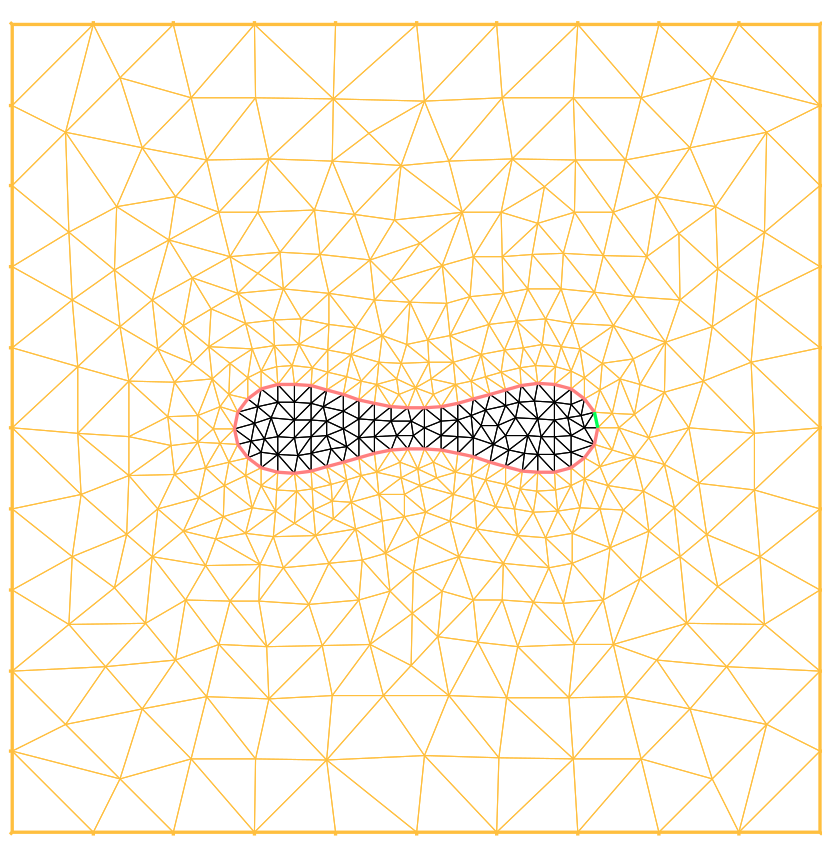
La simulation de la dynamique des globules rouges dans un cadre bidimensionnel permet de reproduire divers comportements connus : Chenille de char, culbute, parachute.
Valves aortiques
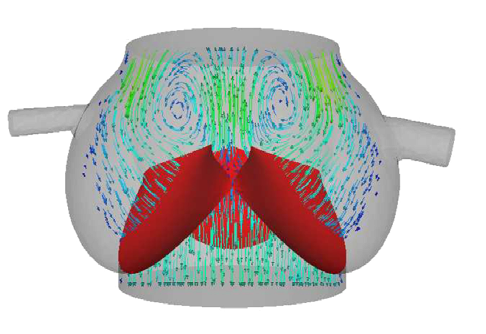
Simulation du comportement des valves aortiques en 3D. La stratégie proposée est basée sur un découplage des solveurs fluides (pour le sang) et solides (pour les valves), chacun d'eux échangeant des informations sur les forces et déplacements. Les contacts entre valves sont gérés par un algorihtme d'approximation interne.
Vesicules

L'énergie de Helfrich qui régit le comportement mécanique des membranes bilipidques des vésicules est obtenue comme limite d'un solide élastique tridimensionnel fortement anisotrope. Une formulation Eulérienne permet de généraliser ce modèle en faisant intervenir la moyenne de la courbure. Selon les paramètres choisis, différentes formes typiques des vésicules peuvent être obtenues.
Plaques isométriques
Le modèle de plaque isométrique est obtenu comme $\Gamma$-limite de l'élasticité non linéaire. Le résultat est basé sur un théorème de rigidité de F. John, amélioré depuis par G. Friesecke, RD. James et S. Müller.
Poutres
Le modèle de poutres non linéaires en flexion/torsion est obtenu comme limite d'un modèle tridimensionnel. On montre en particulier que le coefficient de torsion est obtenu suite à la résolution d'une équation de Poisson sur une section de la poutre.
Réseaux carrés
Détermination du comportement limite d'un réseau périodique carré d'atomes ou de barres avec interactions à trois points lorsque la période du réseau tend vers zéro.
Auto-contacts
Une nouvelle modélisation des contacts sans frottement en déformations finies basée sur un critère topologique satisfait par toute déformation sans auto-intersection. Cette dernière s'applique autant aux structures épaisses qu'aux structures minces.
Approx. Interne
Une méthode d'approximation interne des déformations finies avec contact basée sur l'introduction de multiplicateurs de Lagrange.
Auto-Intersections
En s'inspirant des problèmes de type changement de phase, on définit diverses pénalisations de la contrainte de non auto-intersection. La minimisation de l'énergie pénalisée peut alors être effectuée par un algorithme classique de type gradient.