$$
\left\{
\begin{array}{l}
\dot f = - \alpha g f \\
\dot g = \alpha g f - \beta g \\
\dot h = \beta g
\end{array}\right.
$$
$$2\pi=6.28318530718\cdots$$
$$\sqrt 2=1.41421356237\cdots$$
$$\sum_{n=0}^\infty \frac 1 {n}=+\infty$$
$$1+\frac 1 2 + \frac 1 4 + \frac 1 8 + \cdots = 2$$
$$e^{i\pi}=-1$$
$$\ln(1-x)=-x-\frac{x^2} 2-\frac{x^3}3 - \cdots$$
$$\sin(x)=x-\frac{x^3} 6+\frac{x^5}{120} + \cdots$$
$$\lim_{n\rightarrow \infty}(1+x/n)^n=e^x$$
$$\frac{\pi^2} 6=\sum_n \frac 1 {n^2}$$
$$\lim_{x\rightarrow 0} \frac{f(x)}{g(x)}=\frac{f'(x)}{g'(x)}$$
$$x_{n+1}=x_n-h \nabla J(x_n)$$
$$e^{x+y}=e^xe^y$$
$$f'(x)=\lim_{h\rightarrow 0}\frac{f(x+h)-f(x)} h$$
Analyse et méthodes numériques
Fonctions réelles
IUT Nice Sophia-Antipolis
Fonctions réelles
$$
f : \mathbb R \rightarrow \mathbb R^n
$$
$$
f : D(f) \rightarrow \mathbb R^n
$$
$\cos(x)$
$x^2$
$e^x$
$1/x$
$$
D(f)=\mathbb R^*
$$
$t=$ $0$$1$$2$$3$$4$$5$$6$$7$$8$$9$ $0$$1$$2$$3$$4$$5$$6$$7$$8$$9$$s$
$$
\left\{
\begin{array}{ll}
\dot v(t)=(0,-g) & \text{ pour }t\in [0,T] \\
\dot x(t)=v(t) & \text { pour }t\in [0,T]\\
x(0)=x_0\\
v(0)=v_0
\end{array}
\right.
$$
$x(t)$ = position du boulet au temps $t$
$v(t)$ = vitesse du boulet au temps $t$
$v(t)$ = vitesse du boulet au temps $t$
Cliquer sur le canon
Épidémie
$$
\left\{
\begin{array}{l}
\dot f = - \alpha g f \\
\dot g = \alpha g f - \beta g \\
\dot h = \beta g
\end{array}\right.
$$
$f$ = Proportion non contaminés
$g$ = Contaminés et contagieux
$h$ = Contaminés, non contagieux (décédés ou guéris).
$g$ = Contaminés et contagieux
$h$ = Contaminés, non contagieux (décédés ou guéris).
Épidémie
| $T$ | $=$ | |
| $\alpha$ | $=$ | |
| $\beta$ | $=$ | |
| $g_0$ | $=$ | |
| $h_0$ | $=$ |
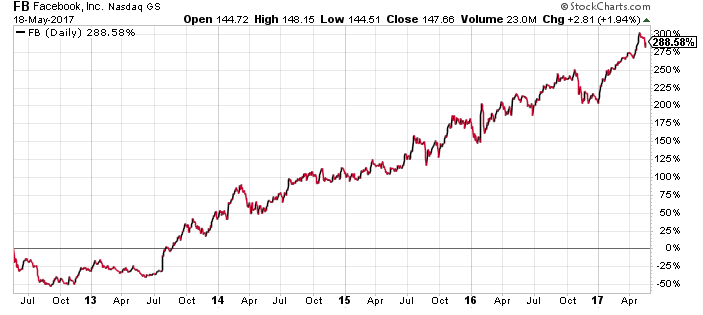
Finance
Notation
$$
\begin{array}{rrcl}
f:&D(f)&\rightarrow& \mathbb R \\
&x&\mapsto& f(x)
\end{array}
$$
Définition Limite
$$
\lim_{x\rightarrow a} f(x)=\ell
$$
ssi $\forall (x_n) \in \mathbb R^{\mathbb N}$ tel que $x_n\rightarrow a$,
$$
\lim f(x_n)=\ell.
$$
Définition Limite 2
$$
\lim_{\begin{array}{c} x\rightarrow a \\ \color{red}{x\in A} \end{array}} f(x)=\ell
$$
ssi $\forall (x_n) \in \color{red}A^{\mathbb N}$ tel que $x_n\rightarrow a$,
$$
\lim f(x_n)=\ell.
$$
Définition Limite 3
Si $f:\mathbb R \rightarrow \color{red}{\mathbb R^n}$,
$$
\lim_{\begin{array}{c} x\rightarrow a \end{array}} f(x)=\ell
$$
ssi $\forall (x_n)$ tel que $x_n\rightarrow a$,
$$
\color{red}{\forall i \in \{1,\cdots,n\}}, \lim f_{\color{red} i}(x_n)=\ell_{\color{red} i}.
$$
Exemples de limites
$$
\lim_{x\rightarrow 0} \sin(x)=0
$$
$$
\lim_{x\rightarrow 0} (1+x)^{1/x}=e
$$
$$
\lim_{\begin{array}{c} x\rightarrow 0 \\ x\in \mathbb R_+ \end{array}} 1/x=+\infty
$$
$$
\lim_{x\rightarrow 0}\left( \begin{array}{c} x \\ (x+1)^2 \end{array}\right) =
\left( \begin{array}{c} 0 \\ 1 \end{array}\right)
$$
Continuité
$f$ est continue en $a$ ssi
$$
\lim_{x \rightarrow a} f(x)=f(a).
$$
Continuité Globale
$f$ est dit continue ssi
$f$ est continue en tout $x\in D(f).$
$\cos(x)$
$x^2$
$e^x$
$1/x$
Mouvement brownien
Partie entière $E(x)$
Notation
$\mathcal C(X)$= Fonctions continues sur $X$
à valeurs dans $\mathbb R$.
à valeurs dans $\mathbb R$.
Prolongement
par continuité
Adhérence d'un ensemble
$$
\overline D=\big\{x \in \mathbb R~:~\exists (x_n) \in D^{\mathbb N}\text{ tel que }
x_n\rightarrow x\big\}.
$$
$$ \overline{]0,1]}=[0,1] $$
$$ \overline{\mathbb R^*}=\mathbb R $$
$$ \overline{]a;\infty[}=[a;\infty[ $$
Définition
$f$ est prolongeable par continuité en $x^*\in \overline {D(f)}$
$$ \exists \ell\in\mathbb R \text{ tel que }
\lim_{\begin{array}{c}x\rightarrow x^*\\x \in D(f)\end{array}} f(x) =\ell.
$$
On pose alors
$$
f(x^*)=\ell.
$$
$(1+x)^{1/x}$ prolongeable en $x=0$ ?
$1/x$
Dérivabilité
$x^2$
cliquer sur la droite
$
\frac{f(\color{#99ee99} x)-f(\color{#9999ee}y)}{\color{#99ee99} x-\color{#9999ee}y}
$
Taux d'accroissement entre $\color{#99ee99} x$ et $\color{#9999ee} y$.
Pente de la droite
$$
\frac{f(\color{#99ee99} x)-f(\color{#9999ee}y)}{\color{#99ee99} x-\color{#9999ee}y}
\xrightarrow{
\begin{array}{c}
\color{#9999ee}y \rightarrow \color{#99ee99} x\\
\end{array}
}f'(\color{#99ee99} x)
$$
$f$ est dite dérivable en $\color{#99ee99} x$
de dérivée $f'(\color{#99ee99} x)$
de dérivée $f'(\color{#99ee99} x)$
$|x|$
$x\mapsto |x|$ n'est pas dérivable en $x=0$.
Règles de dérivation
$$
(\alpha f+g)'=\alpha f'+g'
$$
$$
(fg)'=f'g+fg'
$$
$$
(f\circ g)'=(f'\circ g) g'
$$
$$
(f^{-1})'=1/(f'\circ f^{-1})
$$
Dérivées Classiques
$$
(x^n)'=n x^{n-1}
$$
$$
\cos'(x)=-\sin(x)
$$
$$
\sin'(x)=\cos(x)
$$
$$
(e^x)'=e^x
$$
$$
(\ln(x))'=1/x
$$
Ordre supérieur
Si $f'$ est dérivable, on note $f''$ sa dérivée.
$f''$ est la dérivée seconde de $f$.
Autre notation
$$
f^{(2)}=f''
$$
Don't stop me now...
$$
f^{(n+1)}=(f^{(n)})'
$$