Shape Optimization for Additive Manufacturing
G. Allaire, P. Geoffroy, O. Pantz, K. Trabelsi
Motivation
Compliance minimization
?
Level Set
SIMP
3D printed shape

Otimization Pb
IMPOSSIBLE
$$
-\nabla\cdot A e(u)=f
$$
$$
-\nabla\cdot A^* e(u)=\theta f
$$
Homogenization
Sequence $\Omega_\varepsilon$
$\varepsilon=$16.00
A 1+2 steps program
Step 0 - Preprocessing
Compute $A^*(\alpha,m)$
Step 1 - Homogenization
Compute optimal $(\alpha,m)$
Step 2 - Dehomogenization
$$
\Omega_\varepsilon \rightarrow (\alpha,m)
$$
Step 0 - Computing $A^*$
$\omega=(0,1)^2$-periodic
$\omega \cap (0,1)^2$
Correctors
$$
w_{ij}:=\textrm{argmin} \int_{\Omega} A(e_{ij}+e(w)):(e_{ij}+e(w))
$$
$e_{ij}=e_i\otimes e_j$
Compression along $e_1$
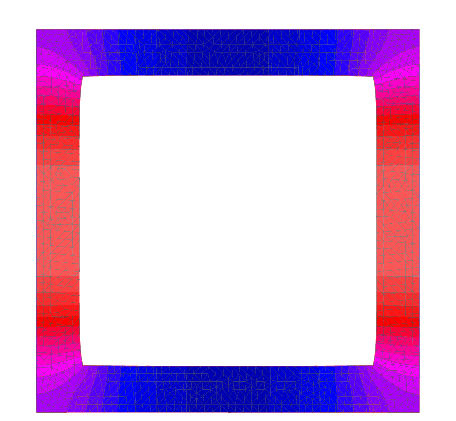
$w_{11}$

$w_{11}$
Compression along $e_2$
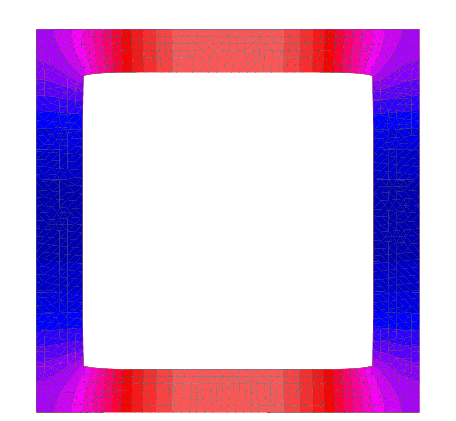
$w_{22}$

$w_{22}$
Shearing
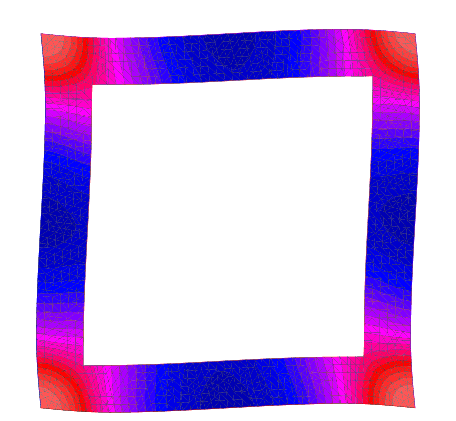
$w_{12}$

$w_{12}$
Hooke's law
$$
A^*_{ijkl}:=\int_{\Omega} A(e_{ij}+e(w_{ij})):(e_{kl}+e(w_{kl}))
$$
$m_1$
$m_2$
$\small A^*(m_1,m_2)$
$\small A^*(m_1,m_2,\alpha)$
$\small = S(\alpha)^TA^*(m_1,m_2)S(\alpha)$
Step 1 : Homogenization
Compliance
$$
\min_{\alpha,m} \left\{J^*(\theta,A^*):=\int_\Omega A^*e(u^*):e(u^*)\,dx\right\}
$$
$$ \int_D \theta\,dx \leq V $$
$$ \int_D \theta\,dx \leq V $$
Stress Formulation
$$
\inf_{m,\sigma} J^*(m,\alpha) = \inf_{\alpha,m,\sigma} \int_D (A^*)^{-1}(m,\alpha) \sigma\cdot \sigma \,dx.
$$
$$
\left\{
\begin{array}{ll}
\nabla\cdot\sigma=0&\text{in } D\\
\sigma n = g&\text{on }\Gamma_N
\end{array}
\right.
$$
Alternate minimization
- Stress $\sigma$
Solve elasticity problem for current $A^*$.
- Orientation of the cell $\alpha$
Pedersen.
- Size of the micro-holes $m$
One step of gradient method.
Step 2 : Dehomogenization
Sequence of shapes
Grid Map $\varphi$

$D \varphi^{-1}(Y)$-periodic shape
$$
\xrightarrow[\quad\quad]{\varphi}
$$

$Y$-periodic shape $\omega$
Optimal Sequence
Definition of the shape sequence $\Omega_\varepsilon$
$$
\Omega_\varepsilon(\varphi,m)=\left\{x\in D~:~\cssId{phi}{\varphi}(x) \in \cssId{vepsilon}{\varepsilon} \omega(\cssId{m}{m}(x)) \right\}.
$$
$\varphi$ Grid Map
${m}$ parameters of the micro-structure
${\varepsilon}$ length scale
Computation of the grid Map $\varphi$
$D\varphi^{-1}=$periodicity cell$=$$e^r a$
$a=$ Rotation field of the cells of angle $\alpha$
$r=$ Dilatation of the cells
$$
\nabla^T r = \nabla\alpha.
$$
Conformity Condition
$$
\nabla^T r = \nabla\alpha
$$
$$
\Delta \alpha=0
$$
Optimization Steps
- Homogenization
-
Add conformity constaint $\Delta\alpha=0$
- Compute dilatation and grid map
Main features
Post-treatment of the homogenization
Find $\Omega_\varepsilon$ converging toward the optimal composite
$\varepsilon$=Length scale of the fine details
One UNIQUE computation for ALL $\varepsilon$


Thank you for your attention
