In our approach, we now denote by ![]() the image and
the image and ![]() its boundary,
its boundary,
![]() the missing part of the image and
the missing part of the image and ![]() its boundary. Let
its boundary. Let ![]() be the image that we want to restore. We assume that
be the image that we want to restore. We assume that ![]() is known in
is known in
![]() , and unknown in
, and unknown in ![]() .
.
The idea is to adapt the crack localization method to inpainting: crack detection first allows us to identify the cracks (or edges) ![]() of the hidden part
of the hidden part ![]() of the image, and then we will impose that the Laplacian of the restored image is equal to zero in
of the image, and then we will impose that the Laplacian of the restored image is equal to zero in
![]() . For a given crack
. For a given crack
![]() , as
, as ![]() (Dirichlet condition) and
(Dirichlet condition) and
![]() (Neumann condition) are known on the boundary
(Neumann condition) are known on the boundary ![]() of
of ![]() , we can solve two different problems inside
, we can solve two different problems inside ![]() .
.
For a given crack ![]() , we denote by
, we denote by
![]() the solution of the following Dirichlet problem:
the solution of the following Dirichlet problem:
In the same way, if we assume ![]() to be enough regular, we can consider the solution
to be enough regular, we can consider the solution
![]() of the following Neumann problem:
of the following Neumann problem:
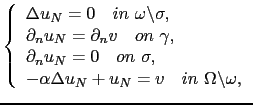 |
(2.13) |