Let ![]() be a bounded open set of
be a bounded open set of
![]() . We assume in this section that
. We assume in this section that ![]() contains a perfectly insulating crack
contains a perfectly insulating crack
![]() . We impose a flux
. We impose a flux
![]() on the boundary
on the boundary ![]() of
of ![]() , and we want to find
, and we want to find
![]() such that the solution
such that the solution
![]() of
of
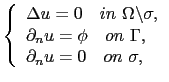 |
(2.7) |
A topological gradient approach has been introduced in [8], and consists of defining a Dirichlet and a Neumann problem, as we have an over-determination in the boundary conditions:
It is clear that for the actual crack
![]() , the two solution
, the two solution ![]() and
and ![]() are equal. The idea is then to consider and minimize the following cost function
are equal. The idea is then to consider and minimize the following cost function
The topological asymptotic expansion of this cost function is detailed in [8].