


Next: Classification
Up: Restoration
Previous: Remarks
Contents
In this section, we adapt the topological gradient approach to color images. Color images can be represented or modeled in various ways, for instance the RGB (Red-Green-Blue) space in which images are viewed as functions from 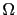 to
to
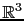 instead of
instead of
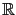 . A first approach consists of decoupling the three channels, and in solving direct and adjoint problems for each channel. But it is also possible to consider directly the vectorial minimization problem, involving the resolution of vectorial problems. The topological asymptotic expansion is still given by equations (2.25-2.26) and (2.28), where all functions are vectorial, i.e. the topological gradient is the sum on all channels of the corresponding expressions for each channel [25].
. A first approach consists of decoupling the three channels, and in solving direct and adjoint problems for each channel. But it is also possible to consider directly the vectorial minimization problem, involving the resolution of vectorial problems. The topological asymptotic expansion is still given by equations (2.25-2.26) and (2.28), where all functions are vectorial, i.e. the topological gradient is the sum on all channels of the corresponding expressions for each channel [25].
Another approach has also been studied in [25], in which we use a different norm for coupling the different channels. In order to identify the local variations of the color image, Di Zenzo defines a multi-spectral tensor associated to the image vector field [55]:
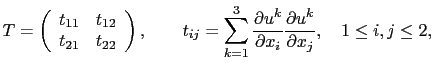 |
(2.30) |
in the case of bidimensional images. This tensor describes the first order differential structure of the image, and the Di Zenzo gradient is given by the square root of the largest eigenvalue of the structure tensor:
![$\displaystyle \Vert\nabla u\Vert _{DZ} = \frac{1}{\sqrt{2}} \left[ t_{11}+t_{22}+\sqrt{(t_{11}-t_{22})^2+4t_{12}^2}\right]^{\frac{1}{2}}.$](img131.png) |
(2.31) |
It is possible to rewrite this gradient in a different way with the following function:
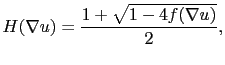 |
(2.32) |
where
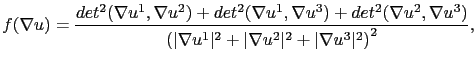 |
(2.33) |
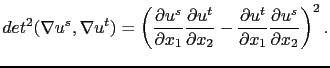 |
(2.34) |
Then, we can derive the asymptotic expansion of the cost function defined by equation (2.24) in which the norm is the Di Zenzo norm (2.31):
![$\displaystyle G(x_0,n) = \sum_{k=1}^3 \left[ -\pi c (\nabla u_0^k(x_0).n)(\nabla v_0^k(x_0).n)-\pi H(\nabla u_0(x_0))\vert\nabla u_0^k(x_0).n\vert^2\right]$](img135.png) |
(2.35) |
with our standard notations.
In [25], we show that this approach has the same computational cost as the vectorial approach (in which the different channels are decoupled), while it improves the edge detection, and hence it produces a better restored image, more precise on the edges of the image.



Next: Classification
Up: Restoration
Previous: Remarks
Contents
Back to home page
![]() to
to
![]() instead of
instead of
![]() . A first approach consists of decoupling the three channels, and in solving direct and adjoint problems for each channel. But it is also possible to consider directly the vectorial minimization problem, involving the resolution of vectorial problems. The topological asymptotic expansion is still given by equations (2.25-2.26) and (2.28), where all functions are vectorial, i.e. the topological gradient is the sum on all channels of the corresponding expressions for each channel [25].
. A first approach consists of decoupling the three channels, and in solving direct and adjoint problems for each channel. But it is also possible to consider directly the vectorial minimization problem, involving the resolution of vectorial problems. The topological asymptotic expansion is still given by equations (2.25-2.26) and (2.28), where all functions are vectorial, i.e. the topological gradient is the sum on all channels of the corresponding expressions for each channel [25].
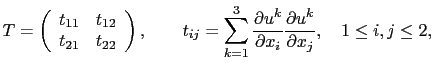
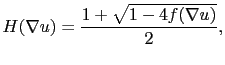
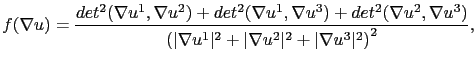
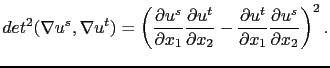
![$\displaystyle G(x_0,n) = \sum_{k=1}^3 \left[ -\pi c (\nabla u_0^k(x_0).n)(\nabla v_0^k(x_0).n)-\pi H(\nabla u_0(x_0))\vert\nabla u_0^k(x_0).n\vert^2\right]$](img135.png)