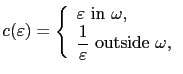 |
(2.40) |
We still consider the restoration algorithm, in which the following conductivity is used for the perturbed problem:
Then we have the following asymptotic result [18]:
| (2.42) |
This result proves that the segmented image ![]() can be approximated by
can be approximated by
![]() if
if
![]() is small. We now assume that the edge set
is small. We now assume that the edge set ![]() is of codimension
is of codimension ![]() in
in ![]() . From the point of view of applications, it is completely natural to assume that the edges are flat in the image. In order to have coherent notations, we will further denote by
. From the point of view of applications, it is completely natural to assume that the edges are flat in the image. In order to have coherent notations, we will further denote by ![]() the edge set. We assume that
the edge set. We assume that ![]() is known, e.g. provided by the crack detection algorithm previously seen.
is known, e.g. provided by the crack detection algorithm previously seen.
We can rewrite the approximated segmentation problem
![]() as follows:
as follows:
| (2.45) |
| (2.46) |
For numerical reasons, it can be very difficult to solve directly problem
![]() , and even problem
, and even problem
![]() for too small values of
for too small values of
![]() . Indeed the conditioning of the system to be solved goes to infinity when
. Indeed the conditioning of the system to be solved goes to infinity when
![]() . In order to overcome this issue, we will expand the solution
. In order to overcome this issue, we will expand the solution
![]() of problem
of problem
![]() into a power series of
into a power series of
![]() .
.