


Next: Algorithm
Up: Segmentation
Previous: From restoration to segmentation
Contents
From the knowledge of the power series expansion of
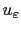 and the computation of several solutions
and the computation of several solutions
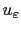 for not too small coefficients
for not too small coefficients
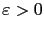 , it is possible to approximate the asymptotic solution
, it is possible to approximate the asymptotic solution 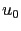 [18]:
[18]:
We can define a function of
 as follows
as follows
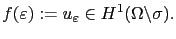 |
(2.51) |
From the previous theorem, we know that 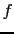 has a power series expansion at the origin given by (2.48). We consider a family of
has a power series expansion at the origin given by (2.48). We consider a family of 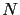 points
points
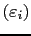 in
in
![$ [\varepsilon_c,\varepsilon_R]$](img185.png) , where
, where
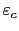 is the smallest value of
is the smallest value of
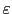 for which it is easy to numerically compute
for which it is easy to numerically compute
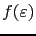 , and
, and
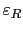 is smaller than the convergence radius of the power series. We can then compute an interpolation polynomial
is smaller than the convergence radius of the power series. We can then compute an interpolation polynomial 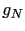 of degree
of degree 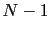 defined by:
defined by:
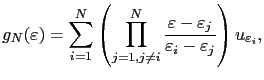 |
(2.52) |
where 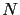 is the number of points
is the number of points
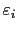 .
.
The analycity of 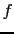 allows us to estimate the approximation error:
allows us to estimate the approximation error:
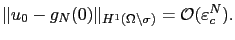 |
(2.53) |



Next: Algorithm
Up: Segmentation
Previous: From restoration to segmentation
Contents
Back to home page
![]() and the computation of several solutions
and the computation of several solutions
![]() for not too small coefficients
for not too small coefficients
![]() , it is possible to approximate the asymptotic solution
, it is possible to approximate the asymptotic solution ![]() [18]:
[18]:
![]() as follows
as follows
![]() allows us to estimate the approximation error:
allows us to estimate the approximation error: