

Next: Preconditioned conjugate gradient
Up: Complexity and speeding up
Previous: Complexity and speeding up
Contents
In all the algorithms we presented in the previous sections, we only have to solve the following PDE
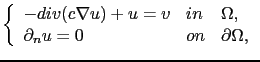 |
(2.54) |
for various coefficients 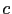 . The first resolutions are done with a constant value of
. The first resolutions are done with a constant value of 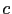 . It is then possible to largely speed up the computation time by using the discrete cosine transform (DCT) method. Problem (2.54) is then equivalent to
. It is then possible to largely speed up the computation time by using the discrete cosine transform (DCT) method. Problem (2.54) is then equivalent to
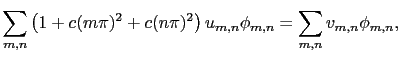 |
(2.55) |
where we denote by
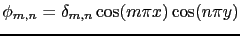 a cosine basis of
a cosine basis of
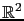 , and where
, and where 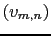 represent the DCT coefficients of the original image
represent the DCT coefficients of the original image 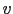 . It is then straightforward to identify
. It is then straightforward to identify 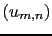 , the DCT coefficients of
, the DCT coefficients of 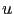 in equation (2.55):
in equation (2.55):
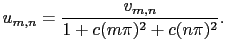 |
(2.56) |
The complexity of such a resolution is
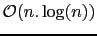 , where
, where 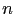 is the number of pixels of the image. The resolution of all unperturbed problems is then done in the following way:
is the number of pixels of the image. The resolution of all unperturbed problems is then done in the following way:
- Computation of
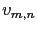 , the DCT coefficients of the original image
, the DCT coefficients of the original image 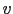 .
.
- Computation of
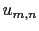 , the DCT coefficients of
, the DCT coefficients of 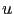 from equation (2.56).
from equation (2.56).
- Computation of
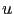 using an inverse DCT.
using an inverse DCT.



Next: Preconditioned conjugate gradient
Up: Complexity and speeding up
Previous: Complexity and speeding up
Contents
Back to home page