


Next: Coupling between the topological
Up: Complexity and speeding up
Previous: Discrete cosine transform
Contents
Then, the solution of all previously detailed problems comes from the resolution of a perturbed problem. For the last resolution of a direct problem with a non constant coefficient 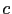 , we can rewrite the problem in the following way:
, we can rewrite the problem in the following way:
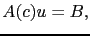 |
(2.57) |
where 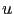 is the unknown image. If
is the unknown image. If 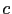 is constant, equation (2.57) is easy to solve. The idea is to precondition equation (2.57) with the DCT solver used in the first resolution. Problem (2.57) is equivalent to
is constant, equation (2.57) is easy to solve. The idea is to precondition equation (2.57) with the DCT solver used in the first resolution. Problem (2.57) is equivalent to
![$\displaystyle \left[A(c_0)^{-1}A(c)\right] u = \left[ A(c_0)^{-1}B \right].$](img212.png) |
(2.58) |
As 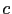 is close to
is close to 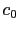 (
(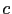 is indeed equal to
is indeed equal to 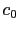 , except in a negligible part of the domain), the system matrix
, except in a negligible part of the domain), the system matrix
![$ [A(c_0)^{-1}A(c)]$](img213.png) is close to the identity operator, and the resolution of (2.58) is then easy: we use a preconditioned conjugate gradient (PCG) method to solve this problem. As the coefficient
is close to the identity operator, and the resolution of (2.58) is then easy: we use a preconditioned conjugate gradient (PCG) method to solve this problem. As the coefficient 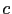 is close to
is close to 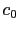 , we can expect a
, we can expect a
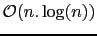 complexity for the resolution of the perturbed problem. The numerical experiments clearly confirm this complexity, both for small and large problems.
complexity for the resolution of the perturbed problem. The numerical experiments clearly confirm this complexity, both for small and large problems.
The main advantage is that it allows us to process images in a very short time (e.g.
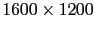 images in less than one second) and movies in real time (provided the movie is split into short sequences of a few seconds) with a c++ code.
images in less than one second) and movies in real time (provided the movie is split into short sequences of a few seconds) with a c++ code.



Next: Coupling between the topological
Up: Complexity and speeding up
Previous: Discrete cosine transform
Contents
Back to home page
![]() , we can rewrite the problem in the following way:
, we can rewrite the problem in the following way:
![]() images in less than one second) and movies in real time (provided the movie is split into short sequences of a few seconds) with a c++ code.
images in less than one second) and movies in real time (provided the movie is split into short sequences of a few seconds) with a c++ code.