next up previous contents
Next: Fast marching Up: Coupling between the topological Previous: Coupling between the topological   Contents

Minimal paths

Let $ g$ be the topological gradient. The idea of the minimal path technique is to define a potential function, measuring in some sense for any point of $ \Omega$ the cost for a path to contain this point. As we want to identify paths in the most negative part of the topological gradient, and considering that the potential function must be positive, we define the following function:

$\displaystyle P(x) = g(x) - \min_{y\in\Omega} \left\{ g(y) \right\}.$ (2.59)

We simply shift the topological gradient from its minimal value, in order to obtain a positive function. We can see that the points where the topological gradient $ g$ reaches its minimal value are costless. This is a way to consider that these points must be on the minimal paths.

We denote by $ C(s)$ a path (or curve) in the image, where $ s$ represents the curvilign coordinate. We can now define a cost function, measuring the cost of such a path:

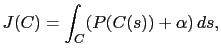$\displaystyle J(C) = \int_C (P(C(s))+\alpha)\,ds,$ (2.60)

where $ \alpha>0$ is a positive regularization coefficient, measuring the length of this path.

The goal is to minimize $ J$ , in order to find the shortest and least costly path between two points. For this purpose, we define the following distance function:

$\displaystyle D(x;x_0) = \inf_{C\in\mathcal{A}(x,x_0)} J(C),$ (2.61)

where $ \mathcal{A}(x,x_0)$ is the set of all paths going from $ x_0$ to $ x$ in the image.

next up previous contents
Next: Fast marching Up: Coupling between the topological Previous: Coupling between the topological   Contents
Back to home page