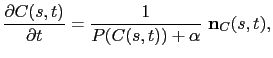 |
(2.62) |
The fastest way to compute the distance function defined by equation (2.61) is to solve a front propagation equation:
This path evolves with a propagation speed inversely proportional to the potential function. If for example a point in the outer part of the front has a large potential (i.e. a large cost), then the propagation speed will be nearly equal to 0
and the front will not expand at this point. From the theory of Eikonal equations, the distance ![]() is simply the instant
is simply the instant ![]() at which the front, initialized at point
at which the front, initialized at point ![]() , reaches point
, reaches point ![]() [118,56].
[118,56].