next up previous contents
Next: Numerical experiments Up: Choice of the nudging Previous: Sequential interpretation   Contents

Pole assignment method and backward nudging matrix

The goal of the backward nudging term is both to have a backward data assimilation system and to stabilize the integration of the backward system (3.4), as this system is usually ill posed. The choice of the backward nudging matrix is then imposed by this stability condition.

If we consider a linearized situation, in which the system and observation operators ($ F$ and $ C$ , respectively) are linear, and if we make the change of time variable $ t'=T-t$ , then the backward equation can be rewritten as

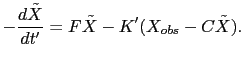$\displaystyle -\frac{d\tilde{X}}{dt'} = F\tilde{X}-K'(X_{obs}-C\tilde{X}).$ (3.10)

Then, the matrix to be stabilized is $ -F-K'C$ , i.e. the eigenvalues of this matrix should have negative real parts.

We now recall the pole assignment result (see e.g. [53,11,41,108]):

Theorem 3.1   If $ (F,C)$ is an observable system, where $ F$ is a $ n\times n$ matrix and $ C$ is a $ m\times n$ matrix (here $ n$ is the size of the control vector $ X$ and $ m$ is the size of the observation vector $ X_{obs}$ ), then there exists at least one matrix $ K'$ such that $ -F-K'C$ is a Hurwitz matrix, i.e. all its eigenvalues are in the negative half-plane.

We should also recall that $ (F,C)$ is an observable system if and only if the rank of $ [C,CF,\dots,CF^{n-1}]$ is equal to $ n$ . Hence, we can assume that there exists at least one matrix $ K'$ such that the backward nudging system (3.4) is stable. However, such a matrix $ K'$ may be hard to compute, as it usually requires the resolution of a Riccati equation.

next up previous contents
Next: Numerical experiments Up: Choice of the nudging Previous: Sequential interpretation   Contents
Back to home page