next up previous contents
Next: Layered quasi-geostrophic ocean model Up: Physical models Previous: 1-D viscous Burgers' equation   Contents

Shallow water model

The shallow water model (or Saint-Venant's equations) is a basic model, representing quite well the temporal evolution of geophysical flows. This model is usually considered for simple numerical experiments in oceanography, meteorology or hydrology. The shallow water equations are a set of three equations, describing the evolution of a two-dimensional horizontal flow. These equations are derived from a vertical integration of the three-dimensional fields, assuming the hydrostatic approximation, i.e. neglecting the vertical acceleration. There are several ways to write the shallow water equations, considering either the geopotential or height or pressure variables. We consider here the following configuration:

$\displaystyle \left\{ \begin{array}{l} \displaystyle \partial_t u - (f+\zeta)v+... ... \\ [0.3cm] \partial_t h+\partial_x(hu)+\partial_y(hv) = 0, \end{array} \right.$ (3.15)

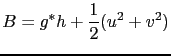where $ \zeta=\partial_x v-\partial_y u$ is the relative vorticity, $ \displaystyle B = g^\ast h+\frac{1}{2}(u^2+v^2)$ is the Bernoulli potential, $ g^\ast$ is the reduced gravity, $ f$ is the Coriolis parameter (in the $ \beta$ -plane approximation), $ \rho_0$ is the water density, $ r$ is the friction coefficient, and $ \nu$ is the viscosity (or dissipation) coefficient. The unknowns are $ u$ and $ v$ the horizontal components of the velocity, and $ h$ the geopotential height. Finally, $ \tau$ is the forcing term of the model (e.g. the wind stress) [38].

Many numerical experiments and comparisons with the variational scheme are presented in [17]. This article also reports the results of an hybridization between the BFN and variational schemes.

next up previous contents
Next: Layered quasi-geostrophic ocean model Up: Physical models Previous: 1-D viscous Burgers' equation   Contents
Back to home page