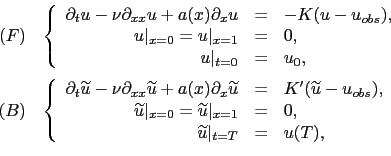Linear viscous transport

Next: Viscous Burgers Up: Transport equations Previous: Transport equations Contents

Linear viscous transport

We first consider a linear viscous transport equation.

$\begin{displaymath}\begin{array}{rl} (F) & \left\{ \begin{array}{rcl} \partial_t... ...etilde{u}\vert _{t=T} &=& u(T), \end{array} \right. \end{array}\end{displaymath}$

(3.25)

where the following notations hold for all further cases:

the time period considered here is $t\in[0,T]$ ;
the first equation is called the forward equation, the second one is called the backward one;
and $K^\prime$ are positive functions, and may depend on and , but for simplicity reasons, we will always assume that there exists a constant $\kappa \in \mathbb{R}_{+}^*$ such that $K^\prime(t,x) = \kappa K(t,x)$ ;
$a(x)\in W^{1,\infty}(\Omega)$ , $\Omega$ being the considered space domain, either the interval or the torus ;
the viscosity coefficient $\nu>0$ is constant;
the observation function $u_{obs}$ is a solution of the forward equation (without any nudging term) with initial condition $u_{obs}^0$ :

$\displaystyle \left\{ \begin{array}{rcl} \partial_t u_{obs} -\nu \partial_{xx} ... ...rt _{x=0}=u\vert _{x=1}&=&0,\\ u\vert _{t=0} &=& u_{obs}^0. \end{array} \right.$ (3.26)

Then, the following result holds true for linear viscous transport equations [29]:

Theorem 3.3 We consider one step of the BFN algorithm (3.25) with observations $u_{obs}$ satisfying equation (3.26). We denote

$\begin{displaymath}\begin{array}{rcl} w(t) &=& u(t) - u_{obs}(t), \\ \widetilde{w}(t) &=& \widetilde{u}(t)-u_{obs}(t), \end{array}\end{displaymath}$

(3.27)

the forward and backward errors.

If , then for all $t\in[0,T]$ :

$\displaystyle \widetilde{w}(t) = e^{(-K-K^\prime)(T-t)} w(t).$ (3.28)
If , with $\textrm{Support }(K) \subset [a,b]$ where and $a\neq 0$ or $b\neq 1$ , then equation (3.25) is ill-posed: there does not exist a solution $(u,\widetilde{u})$ in general.
If $K(t,x)=K \mathbbm{1}_{[t_{1},t_{2}]}(t)$ with $0\leq t_{1} < t_{2}\leq T$ , then we have

$\displaystyle \widetilde{w}(0) = e^{(-K-K^\prime)(t_{2}-t_{1})} w(0).$ (3.29)

This result shows that, when applied to linear viscous transport equations, the BFN algorithm converges if the feedback acts on the entire domain. For instance, in the first point of theorem 3.3, equation (3.28) shows that the error has been decreased by a factor of $e^{(-K-K')T}$ during one iteration. Thus, the error decreases by a factor of $e^{-N(K+K')T}$ during iterations. As (or ) and , this clearly proves the convergence of the BFN algorithm in this case. On the contrary, if a part of the space domain is not observed (i.e. the support of does not cover the entire domain), then the algorithm does not converge as the diffusion term cannot be controlled and the backward resolution is ill-posed.

Next: Viscous Burgers Up: Transport equations Previous: Transport equations Contents

Back to home page