next up previous contents
Next: Invariant correction terms Up: Nudging and observers Previous: Nudging and observers   Contents

Observers for a shallow water model

We consider here a shallow water model, similar to the model introduced in section 3.3.3. However, the equations are rewritten in order to clearly see the symmetries. We refer to [72] for more details about these equations. In the following, 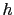$ h$ is the fluid height, and 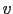$ v$ is the bi-dimensional velocity field. The equations write:

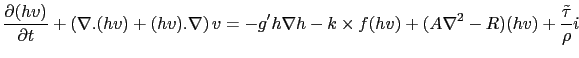$\displaystyle \frac{\partial(hv)}{\partial t} + \left( \nabla . (hv) + (hv) . \... ... \nabla h - k \times f(hv) + (A \nabla^2 - R)(hv) + \frac{\tilde{\tau}}{\rho} i$ (3.48)

for the vectorial velocity, and

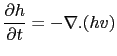$\displaystyle \frac{\partial h}{\partial t} = -\nabla . (hv)$ (3.49)

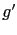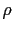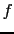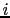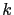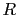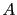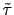for the scalar height. In these equations, $ g'$ represents the reduced gravity, $ \rho$ is the fluid density, $ f$ is the Coriolis parameter, $ i$ is the longitudinal unit vector (pointing towards East) and $ k$ is the upward unit vector. Finally, $ R$ , $ A$ and $ \tilde{\tau}$ represent friction, lateral viscosity, and the forcing term (zonal wind stress) respectively.

We assume that the physical system is observed by several satellites that provide measurements of the sea surface height (SSH) 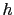$ h$ only.

An observer 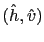$ (\hat{h},\hat{v})$ for the system (3.48-3.49) writes:

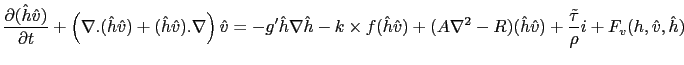$\displaystyle \frac{\partial(\hat{h}\hat{v})}{\partial t} + \left( \nabla . (\h... ...a^2 - R)(\hat{h}\hat{v}) + \frac{\tilde{\tau}}{\rho} i + F_v(h,\hat{v},\hat{h})$ (3.50)

and

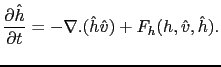$\displaystyle \frac{\partial \hat{h}}{\partial t} = -\nabla . (\hat{h}\hat{v}) + F_h(h,\hat{v},\hat{h}).$ (3.51)

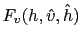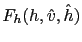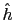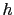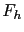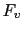The only difference between the observer and model equations comes from the innovation terms $ F_v(h,\hat{v},\hat{h})$ and $ F_h(h,\hat{v},\hat{h})$ . The correction terms must vanish when the estimated height $ \hat h$ is equal to the observed height $ h$ . The goal is to define functions $ F_h$ and $ F_v$ such that the observer tends to the true solution. Moreover, these feedback terms also have to preserve the symmetries of the model.

next up previous contents
Next: Invariant correction terms Up: Nudging and observers Previous: Nudging and observers   Contents
Back to home page