


Next: Convergence study on a
Up: Nudging and observers
Previous: Observers for a shallow
Contents
The shallow-water equations do not depend neither on the orientation nor on the origin of the frame in which the coordinates are expressed: they are invariant under the action of 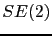 , the Special Euclidean group of isometries of the plane
, the Special Euclidean group of isometries of the plane
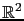 . Consequently, functions
. Consequently, functions 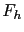 and
and 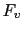 must be invariant under the action of
must be invariant under the action of 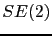 . Symmetries have been very recently introduced for observer design in [1,40] for engineering problems. The aim of this work is to consider correction terms that respect the underlying physics of the system.
. Symmetries have been very recently introduced for observer design in [1,40] for engineering problems. The aim of this work is to consider correction terms that respect the underlying physics of the system.
To find the scalar term 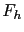 , we use the standard result (see e.g. [98]), which states that any scalar differential operator invariant by rotation and translation writes
, we use the standard result (see e.g. [98]), which states that any scalar differential operator invariant by rotation and translation writes 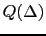 , where
, where 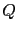 is a polynomial and
is a polynomial and 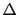 is the Laplacian. By considering the invariance by rotation for the vectorial velocity [87], we get the following family of scalar terms:
is the Laplacian. By considering the invariance by rotation for the vectorial velocity [87], we get the following family of scalar terms:
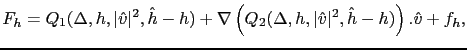 |
(3.52) |
where 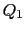 and
and 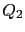 are scalar polynomials in
are scalar polynomials in  , and
, and 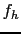 is an integral term defined below. More precisely,
is an integral term defined below. More precisely,
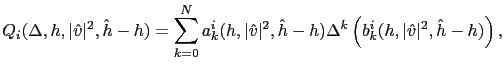 |
(3.53) |
where 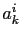 and
and 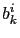 are smooth scalar functions such that
are smooth scalar functions such that
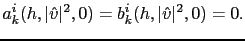 |
(3.54) |
For the vectorial correction term 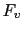 , we use the vectorial counterpart:
, we use the vectorial counterpart:
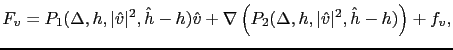 |
(3.55) |
where 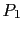 and
and 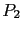 are polynomials in
are polynomials in 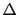 , like
, like 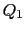 and
and 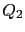 .
.
Let us now find the integral terms 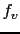 and
and 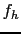 that are invariant by rotation and translation. They can be expressed as a convolution between the previous invariant differential terms and a two-dimensional kernel
that are invariant by rotation and translation. They can be expressed as a convolution between the previous invariant differential terms and a two-dimensional kernel
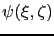 . The previous terms being invariant by rotation, the value of the kernel should not depend on a particular direction, and so
. The previous terms being invariant by rotation, the value of the kernel should not depend on a particular direction, and so 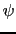 must be a function of the invariant
must be a function of the invariant
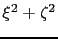 . The integral correction terms write:
. The integral correction terms write:
![$\displaystyle f_v(x,y,t)=\iint \left[ R_1(\Delta,h,\vert\hat{v}\vert^2,\hat{h}-...
...t{h}-h)\right) \right]_{(x-\xi,y-\zeta,t)} \phi_v(\xi^2+\zeta^2)\, d\xi d\zeta,$](img426.png) |
(3.56) |
![$\displaystyle f_h(x,y,t)=\iint \left[ S_1(\Delta,h,\vert\hat{v}\vert^2,\hat{h}-...
...right).\hat{v} \right]_{(x-\xi,y-\zeta,t)} \phi_h(\xi^2+\zeta^2)\, d\xi d\zeta,$](img427.png) |
(3.57) |
where 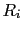 and
and 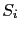 are defined like
are defined like 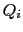 and
and 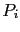 .
.
The support of 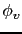 (resp.
(resp. 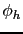 ) is a subset of
) is a subset of
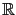 . Its characteristic size defines a zone in which it is significant to correct the estimation with the measurements. The integral formulation is actually quite general: if
. Its characteristic size defines a zone in which it is significant to correct the estimation with the measurements. The integral formulation is actually quite general: if 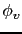 and
and 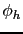 are set equal to Dirac functions, one obtains the differential terms.
are set equal to Dirac functions, one obtains the differential terms.



Next: Convergence study on a
Up: Nudging and observers
Previous: Observers for a shallow
Contents
Back to home page
![]() , the Special Euclidean group of isometries of the plane
, the Special Euclidean group of isometries of the plane
![]() . Consequently, functions
. Consequently, functions ![]() and
and ![]() must be invariant under the action of
must be invariant under the action of ![]() . Symmetries have been very recently introduced for observer design in [1,40] for engineering problems. The aim of this work is to consider correction terms that respect the underlying physics of the system.
. Symmetries have been very recently introduced for observer design in [1,40] for engineering problems. The aim of this work is to consider correction terms that respect the underlying physics of the system.
![]() , we use the standard result (see e.g. [98]), which states that any scalar differential operator invariant by rotation and translation writes
, we use the standard result (see e.g. [98]), which states that any scalar differential operator invariant by rotation and translation writes ![]() , where
, where ![]() is a polynomial and
is a polynomial and ![]() is the Laplacian. By considering the invariance by rotation for the vectorial velocity [87], we get the following family of scalar terms:
is the Laplacian. By considering the invariance by rotation for the vectorial velocity [87], we get the following family of scalar terms:
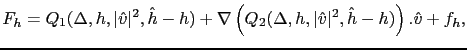
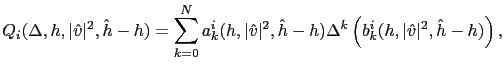
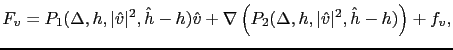
![]() and
and ![]() that are invariant by rotation and translation. They can be expressed as a convolution between the previous invariant differential terms and a two-dimensional kernel
that are invariant by rotation and translation. They can be expressed as a convolution between the previous invariant differential terms and a two-dimensional kernel
![]() . The previous terms being invariant by rotation, the value of the kernel should not depend on a particular direction, and so
. The previous terms being invariant by rotation, the value of the kernel should not depend on a particular direction, and so ![]() must be a function of the invariant
must be a function of the invariant
![]() . The integral correction terms write:
. The integral correction terms write:
![$\displaystyle f_v(x,y,t)=\iint \left[ R_1(\Delta,h,\vert\hat{v}\vert^2,\hat{h}-...
...t{h}-h)\right) \right]_{(x-\xi,y-\zeta,t)} \phi_v(\xi^2+\zeta^2)\, d\xi d\zeta,$](img426.png)
![$\displaystyle f_h(x,y,t)=\iint \left[ S_1(\Delta,h,\vert\hat{v}\vert^2,\hat{h}-...
...right).\hat{v} \right]_{(x-\xi,y-\zeta,t)} \phi_h(\xi^2+\zeta^2)\, d\xi d\zeta,$](img427.png)
![]() (resp.
(resp. ![]() ) is a subset of
) is a subset of
![]() . Its characteristic size defines a zone in which it is significant to correct the estimation with the measurements. The integral formulation is actually quite general: if
. Its characteristic size defines a zone in which it is significant to correct the estimation with the measurements. The integral formulation is actually quite general: if ![]() and
and ![]() are set equal to Dirac functions, one obtains the differential terms.
are set equal to Dirac functions, one obtains the differential terms.