Convergence study on a linearized simplified system

Next: Numerical experiments Up: Nudging and observers Previous: Invariant correction terms Contents

Convergence study on a linearized simplified system

In order to avoid the amplification of the measurement noise by a differentiation process, only the integral correction terms are kept: one sets , and $S_2=R_1=h-\hat{h}$ .

For the sake of clarity, we now simplify the model equations, by assuming that there is no Coriolis force, no friction, no dissipation, and no wind stress. An observer for this simplified system satisfies then:

$\displaystyle \frac{\partial \hat{h}}{\partial t}$	$\displaystyle =$	$\displaystyle -\nabla(\hat{h}\hat{v})+\phi_h \ast (h-\hat{h}),$	(3.58)
$\displaystyle \frac{\partial \hat{v}}{\partial t}$	$\displaystyle =$	$\displaystyle -\hat{v}\nabla \hat{v}-g\nabla \hat{h}+\phi_v\ast\nabla(h-\hat{h}).$	(3.59)

Note that in the degenerate case where $\phi_h=K_h\delta_0$ and $\phi_v=K_v\delta_0$ , and being positive scalars, we find the standard nudging terms, or Luenberger observer.

As it seems difficult to first study the convergence on the nonlinear system, we now linearize the equations around an equilibrium position $h=\bar h$ and $v=\bar v$ . We only consider small velocities $\delta v = v-\bar{v} \ll \sqrt{g\bar{h}}$ and heights $\delta h = h - \bar{h} \ll \bar{h}$ , where $\bar{h}$ and $\bar{v}=0$ represent the equilibrium height and speed respectively. We denote by $\tilde h$ (resp. $\tilde v$ ) the estimation errors, differences between the observer and true solution, for the height (resp. velocity). These errors are solution of the following linear equations:

$\displaystyle \frac{\partial \tilde{h}}{\partial t}$	$\displaystyle =$	$\displaystyle -\bar{h}\nabla \tilde{v}-\phi_h \ast \tilde{h},$	(3.60)
$\displaystyle \frac{\partial \tilde{v}}{\partial t}$	$\displaystyle =$	$\displaystyle -g\nabla \tilde{h} -\phi_v \ast \nabla \tilde{h}.$	(3.61)

A reasonable choice for the kernels $\phi_h$ and $\phi_v$ is the following:

$\displaystyle \phi_h(x,y)$	$\displaystyle =$	$\displaystyle \beta_h\,exp(-\alpha_h (x^2+y^2)),$	(3.62)
$\displaystyle \phi_v(x,y)$	$\displaystyle =$	$\displaystyle \beta_v\,exp(-\alpha_v (x^2+y^2)),$	(3.63)

as one usually assumes that the observation error is a white Gaussian noise. However, the following convergence results can be extended to more general kernel functions defined by

$\displaystyle \phi_h(x,y)$	$\displaystyle =$	$\displaystyle (f(x)\ast f(x))\,(f(y)\ast f(y)),$	(3.64)
$\displaystyle \phi_v(x,y)$	$\displaystyle =$	$\displaystyle (g(x)\ast g(x))\,(g(y)\ast g(y)),$	(3.65)

where

and

are smooth even functions, all their Fourier coefficients being strictly positive.

Eliminating the velocity $\tilde v$ in equations (3.60-3.61) leads to a modified damped wave equation with external viscous damping:

$\displaystyle \frac{\partial^2 \tilde{h}}{\partial t^2} = g\bar{h}\Delta \tilde... ...h}\,\phi_v\ast\Delta\tilde{h} - \phi_h\ast\frac{\partial\tilde{h}}{\partial t}.$

(3.66)

Equation (3.67) can be rewritten in the following way:

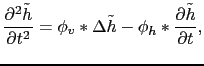$\displaystyle \frac{\partial^2 \tilde{h}}{\partial t^2} = \phi_v\ast\Delta\tilde{h} - \phi_h\ast\frac{\partial\tilde{h}}{\partial t},$

(3.67)

if $\phi_v$ is now the following function

$\displaystyle \phi_v(x,y) = g\bar{h}\delta_0 + \bar{h}\,\beta_v\,exp(-\alpha_v (x^2+y^2)),$

(3.68)

where $\delta_0$ is the Dirac measure at the origin.

Then, we have the following result [22]:

Theorem 3.7

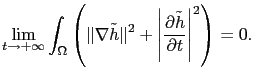$\displaystyle \lim_{t\to +\infty} \int_\Omega \left( \Vert\nabla \tilde{h}\Vert^2 + \left\vert\frac{\partial \tilde{h}}{\partial t}\right\vert^2 \right) = 0.$

(3.69)

This result proves the strong and asymptotic convergence of the error $\tilde h$ towards 0 , and then it also gives the same convergence for $\tilde v$ . We deduce that the observer tends to the true state when time goes to infinity. Note that even if only the height is observed, all variables are corrected.

A dimensional analysis also provides the following gain tuning (see equations (3.62) and (3.69)):

$\displaystyle \beta_h = 2\xi_0\omega_0, \quad \bar h\beta_v = L_0^2\omega_0^2-g\bar{h},$

(3.70)

where $\omega_0$ and

are characteristic pulsation and length of the flow respectively, and $\xi_0$ is the damping coefficient of the system equation. Moreover, $\alpha_h^{-2}=\alpha_v^{-2}$ is the size of the region of influence. This region can be related to the level of observation noise, and to the spatial density of the observations.

Next: Numerical experiments Up: Nudging and observers Previous: Invariant correction terms Contents

Back to home page