


Next: Muti-grid approach and optimization
Up: Description of the algorithm
Previous: Cost function
Contents
The following regularization terms were used in our numerical experiments:
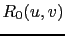 |
 |
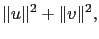 |
(4.4) |
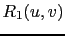 |
 |
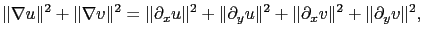 |
(4.5) |
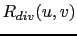 |
 |
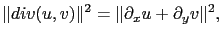 |
(4.6) |
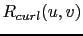 |
 |
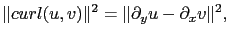 |
(4.7) |
 |
 |
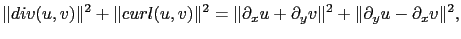 |
(4.8) |
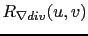 |
 |
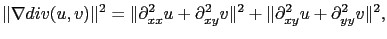 |
(4.9) |
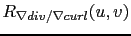 |
 |
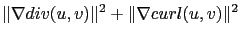 |
(4.10) |
| |
 |
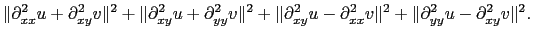 |
|
In all the cases, we can write
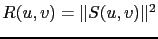 , where
, where 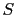 is a linear operator. Some scalar coefficients have also been considered in order to weight the different terms of a given regularization.
is a linear operator. Some scalar coefficients have also been considered in order to weight the different terms of a given regularization.



Next: Muti-grid approach and optimization
Up: Description of the algorithm
Previous: Cost function
Contents
Back to home page