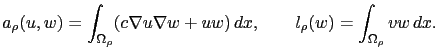


suivant: Gradient topologique
monter: Restauration
précédent: Restauration
Table des matières
Soit
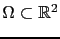 un ouvert borné, et soit
un ouvert borné, et soit
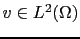 l'image bruitée. Le débruitage d'une image passe généralement par la résolution du problème suivant:
l'image bruitée. Le débruitage d'une image passe généralement par la résolution du problème suivant:
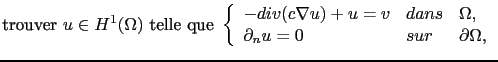 |
(2.21) |
où 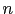 représente la normale unitaire extérieure à
représente la normale unitaire extérieure à
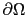 , et
, et 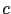 est la conductivité, que nous allons définir par la suite. Différents choix de conductivité sont possibles, essentiellement
est la conductivité, que nous allons définir par la suite. Différents choix de conductivité sont possibles, essentiellement 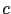 constant (méthode de diffusion linéaire, rapide mais qui rend l'image floue), et
constant (méthode de diffusion linéaire, rapide mais qui rend l'image floue), et 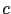 défini par une fonction non linéaire de
défini par une fonction non linéaire de 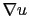 (diffusion non linéaire, qui préserve les contours [115,14]). Dans notre approche,
(diffusion non linéaire, qui préserve les contours [115,14]). Dans notre approche, 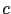 ne prendra que 2 valeurs, soit une valeur de l'ordre de
ne prendra que 2 valeurs, soit une valeur de l'ordre de 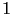 en dehors des contours de l'image afin de lisser l'image, soit 0
sur les contours afin de les préserver.
en dehors des contours de l'image afin de lisser l'image, soit 0
sur les contours afin de les préserver.
Imposer 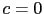 sur une partie de l'image revient à perturber le domaine en insérant des fissures. Pour un point
sur une partie de l'image revient à perturber le domaine en insérant des fissures. Pour un point
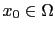 fixé, et pour un paramètre
fixé, et pour un paramètre 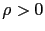 supposé petit, on considère le domaine perturbé
supposé petit, on considère le domaine perturbé
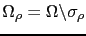 par l'insertion d'une fissure
par l'insertion d'une fissure
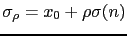 , où
, où 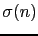 est une fissure de normale unitaire
est une fissure de normale unitaire 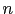 contenant l'origine du domaine. Le problème perturbé peut s'écrire sous la forme variationnelle suivante:
contenant l'origine du domaine. Le problème perturbé peut s'écrire sous la forme variationnelle suivante:
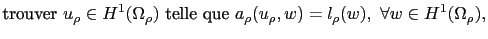 |
(2.22) |
où 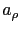 (resp.
(resp. 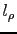 ) est une forme bilinéaire (resp. linéaire) définie sur
) est une forme bilinéaire (resp. linéaire) définie sur
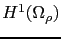 (resp.
(resp.
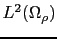 ) par
) par
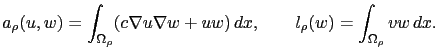 |
(2.23) |
La détection des contours de l'image revient à minimiser par rapport au domaine la fonctionnelle d'énergie suivante:
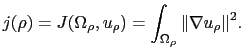 |
(2.24) |

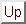


suivant: Gradient topologique
monter: Restauration
précédent: Restauration
Table des matières
Retour à la page principale
![]() un ouvert borné, et soit
un ouvert borné, et soit
![]() l'image bruitée. Le débruitage d'une image passe généralement par la résolution du problème suivant:
l'image bruitée. Le débruitage d'une image passe généralement par la résolution du problème suivant:
![]() sur une partie de l'image revient à perturber le domaine en insérant des fissures. Pour un point
sur une partie de l'image revient à perturber le domaine en insérant des fissures. Pour un point
![]() fixé, et pour un paramètre
fixé, et pour un paramètre ![]() supposé petit, on considère le domaine perturbé
supposé petit, on considère le domaine perturbé
![]() par l'insertion d'une fissure
par l'insertion d'une fissure
![]() , où
, où ![]() est une fissure de normale unitaire
est une fissure de normale unitaire ![]() contenant l'origine du domaine. Le problème perturbé peut s'écrire sous la forme variationnelle suivante:
contenant l'origine du domaine. Le problème perturbé peut s'écrire sous la forme variationnelle suivante: