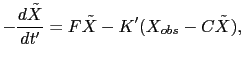next up previous contents
suivant: Expériences numériques monter: Choix des matrices de précédent: Interprétation séquentielle   Table des matières

Méthode de placement de pôles et matrice de nudging rétrograde

Le terme de nudging dans l'équation rétrograde a un double rôle: contraindre le modèle à rester proche des observations, et stabiliser la résolution rétrograde du modèle. En effet, l'irréversibilité des phénomènes physiques considérés fait qu'en général le système rétrograde est instable.

En faisant un changement de variable dans l'équation (3.4) pour se ramener à un temps croissant, on obtient (en supposant une fois encore les opérateurs linéaires):

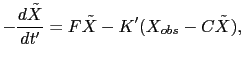$\displaystyle -\frac{d\tilde{X}}{dt'} = F\tilde{X}-K'(X_{obs}-C\tilde{X}),$ (3.10)

avec $ t'=T-t$ . La matrice de stabilité du système est donc $ -F-K'C$ , et la stabilité numérique est garantie si toutes les valeurs propres de cette matrice sont à partie réelle négative.

Le théorème suivant [55,12,42,109], connu sous le nom de méthode de placement de pôles, permet d'obtenir l'existence d'une matrice de nudging rétrograde $ K'$ qui stabilise le système:

Théorème 3.1   Si le système $ (F,C)$ est observable, alors il existe une matrice $ K'$ telle que toutes les valeurs propres de $ -F-K'C$ soient à partie réelle négative.

L'observabilité du système est équivalente au fait que le rang de la matrice
$ [C,CF,\dots,CF^{n-1}]$ est égal à $ n$ , où $ n$ est la dimension du problème physique discrétisé.

Une telle matrice $ K'$ peut parfois être exhibée, à condition de résoudre au préalable des équations du type Riccati, ce qui s'avère relativement coûteux en pratique.

next up previous contents
suivant: Expériences numériques monter: Choix des matrices de précédent: Interprétation séquentielle   Table des matières
Retour à la page principale