next up previous contents
Next: Complexity and speeding up Up: Segmentation Previous: Power series expansion   Contents

Algorithm

We can then define a segmentation algorithm, based on the restoration algorithm previously defined in section 2.4:

$ \bullet$
Solve the direct (2.21) and adjoint (2.27) unperturbed problems with 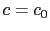$ c=c_0$ everywhere.
$ \bullet$
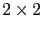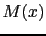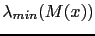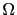Compute the $ 2\times 2$ matrix $ M(x)$ defined by equation (2.28) and its lowest eigenvalue $ \lambda_{min}(M(x))$ at each point of the domain $ \Omega$ .
$ \bullet$
Define 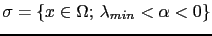$ \sigma=\left\{ x\in\Omega;\, \lambda_{min}<\alpha<0\right\}$ the edge set, where 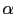$ \alpha$ is a small negative threshold.
$ \bullet$
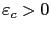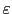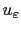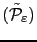Set $ \varepsilon_c>0$ the minimal value of $ \varepsilon$ for which it is easy to compute numerically the solution $ u_\varepsilon$ of problem $ (\tilde{\mathcal{P}}_\varepsilon)$ .
$ \bullet$
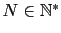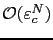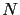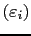Choose $ N\in\mathbb{N}^\ast$ in order to have an approximation error in $ \mathcal{O}(\varepsilon_c^N)$ , and choose $ N$ different values $ (\varepsilon_i)$ .
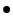
$ \bullet$
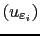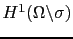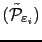Compute the solutions $ (u_{\varepsilon_i})$ in $ H^1(\Omega\backslash\sigma)$ of problems $ (\tilde{\mathcal{P}}_{\varepsilon_i})$ .
$ \bullet$
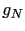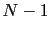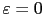Compute the interpolation polynomial $ g_N$ of degree $ N-1$ , defined by equation (2.52), for $ \varepsilon=0$ .

This algorithm has a complexity in 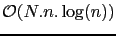$ \mathcal{O}(N.n.\log(n))$ , where 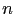$ n$ is the number of pixels in the image, and 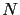$ N$ is the degree of the interpolation approximation. In numerical experiments, 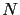$ N$ is typically of the order of 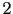$ 2$ to $ 5$ .

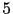Several numerical tests are detailed in [18].

next up previous contents
Next: Complexity and speeding up Up: Segmentation Previous: Power series expansion   Contents
Back to home page