


Next: Inviscid Burgers
Up: Transport equations
Previous: Viscous Burgers
Contents
We now consider the inviscid case for a linear transport equation. The BFN equations are:
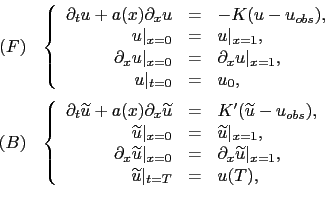 |
(3.32) |
where 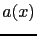 can be constant or not. The following result holds true [29]:
can be constant or not. The following result holds true [29]:
Theorem 3.5
We consider the non viscous one-step BFN (3.32), with observations 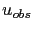 satisfying (3.32-F) with
satisfying (3.32-F) with 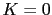 . We denote
. We denote
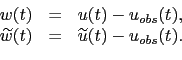 |
(3.33) |
We denote by
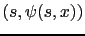 |
(3.34) |
the characteristic curve of equation (3.32-F) with 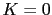 , with foot
, with foot 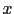 in time
in time 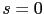 , i.e. such that
, i.e. such that
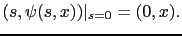 |
(3.35) |
We assume that the final time 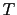 is such that the characteristics are well defined and do not intersect over
is such that the characteristics are well defined and do not intersect over ![$ [0,T]$](img371.png) . Then:
. Then:
- If
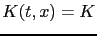 ,
then we have, for all
,
then we have, for all ![$ t\in[0,T]$](img316.png) ,
,
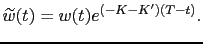 |
(3.36) |
- If
![$ K(t,x)=K \mathbbm{1}_{[t_{1},t_{2}]}(t)$](img349.png) with
with
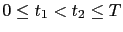 , then we have
, then we have
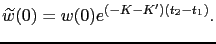 |
(3.37) |
- If
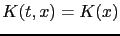 , then we have, for all
, then we have, for all ![$ t\in[0,T]$](img316.png) ,
,
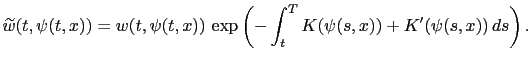 |
(3.38) |
From this result, we deduce that the BFN algorithm applied to inviscid linear transport equation does converge if all the domain is observed (first two cases of theorem 3.5). Moreover, if the support of 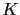 does not cover all the domain (third case of theorem 3.5, e.g. when the system is not fully observed), the algorithm converges as soon as all the characteristics intersect the support of
does not cover all the domain (third case of theorem 3.5, e.g. when the system is not fully observed), the algorithm converges as soon as all the characteristics intersect the support of 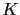 . This constraint is satisfied as soon as the system is observable (see remarks below proposition 3.2).
. This constraint is satisfied as soon as the system is observable (see remarks below proposition 3.2).



Next: Inviscid Burgers
Up: Transport equations
Previous: Viscous Burgers
Contents
Back to home page
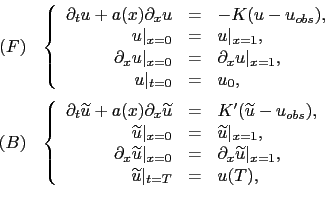
![]() does not cover all the domain (third case of theorem 3.5, e.g. when the system is not fully observed), the algorithm converges as soon as all the characteristics intersect the support of
does not cover all the domain (third case of theorem 3.5, e.g. when the system is not fully observed), the algorithm converges as soon as all the characteristics intersect the support of ![]() . This constraint is satisfied as soon as the system is observable (see remarks below proposition 3.2).
. This constraint is satisfied as soon as the system is observable (see remarks below proposition 3.2).