


Next: Remark:
Up: Transport equations
Previous: Inviscid linear transport
Contents
We finally consider non viscous Burgers' equation, with periodic boundary conditions, and for a time 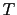 such that there is no shock in the interval
such that there is no shock in the interval ![$ [0,T]$](img371.png) :
:
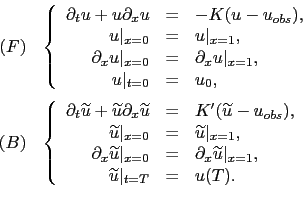 |
(3.39) |
Then, the following result holds true [29]:
Proposition 3.2
We consider one forward (resp. backward) BFN step of the non viscous Burgers' equation (3.39-F) (resp. (3.39-B)). With the notations of theorem 3.6, if
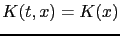 , then we have
, then we have
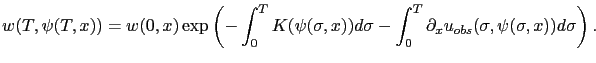 |
(3.44) |
Subsections



Next: Remark:
Up: Transport equations
Previous: Inviscid linear transport
Contents
Back to home page
![]() such that there is no shock in the interval
such that there is no shock in the interval ![]() :
: