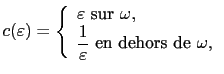 |
(2.40) |
On considère à nouveau l'algorithme de restauration dans lequel on utilise la conductivité suivante pour le problème perturbé:
Nous avons alors le résultat asymptotique suivant [19]:
Ce résultat nous indique qu'on peut approcher l'image segmentée ![]() à l'aide de
à l'aide de
![]() . Désormais, on suppose que
. Désormais, on suppose que ![]() est de co-dimension
est de co-dimension ![]() dans
dans ![]() , ce qui permet de mieux gérer la situation réelle. En effet, du point de vue des applications, il est naturel de considérer que les contours forment un ensemble de dimension
, ce qui permet de mieux gérer la situation réelle. En effet, du point de vue des applications, il est naturel de considérer que les contours forment un ensemble de dimension ![]() lorsque l'image est de dimension
lorsque l'image est de dimension ![]() par exemple. Pour garder la cohérence avec les sections précédentes, nous noterons désormais
par exemple. Pour garder la cohérence avec les sections précédentes, nous noterons désormais ![]() cet ensemble, qui désigne donc les contours de l'image. On suppose que cet ensemble est connu, grâce à la méthode de détection des contours que nous avons vue à plusieurs reprises précédemment.
cet ensemble, qui désigne donc les contours de l'image. On suppose que cet ensemble est connu, grâce à la méthode de détection des contours que nous avons vue à plusieurs reprises précédemment.
Le problème
![]() devient désormais
devient désormais
| (2.45) |
| (2.46) |
La résolution directe du problème
![]() peut s'avérer extrêmement coûteuse en pratique, à cause du très mauvais conditionnement du système. L'idée est alors de résoudre des approximations
peut s'avérer extrêmement coûteuse en pratique, à cause du très mauvais conditionnement du système. L'idée est alors de résoudre des approximations
![]() , et d'approcher la solution
, et d'approcher la solution ![]() à l'aide des solutions
à l'aide des solutions
![]() ainsi construites.
ainsi construites.