next up previous contents
suivant: Algorithme monter: Segmentation précédent: De la restauration à   Table des matières

Développement en série entière

Nous allons nous appuyer sur le développement en série entière de la solution 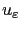$ u_\varepsilon$ pour construire une suite d'approximations [19]:

Théorème 2.4   Il existe une constante $ \varepsilon_R>0$ et une famille de fonction $ (u_n)_{n\in\mathbb{N}}$ de $ H^1(\Omega\backslash\sigma)$ telle que pour tout $ 0\le \varepsilon \le \varepsilon_R$ ,

$\displaystyle u_\varepsilon = \sum_{n=0}^\infty u_n \varepsilon^n.$ (2.48)

De plus, $ u_0$ est l'unique solution du problème $ (\tilde{\mathcal{P}}_0)$ , et les autres fonctions sont les uniques solutions dans $ H^1(\Omega\backslash\sigma)$ des problèmes respectifs suivants:

$\displaystyle (\tilde{\mathcal{P}}_1) \left\{ \begin{array}{lll} -div\left(\... ... sur & \sigma, \partial_n u_1 = 0 & sur & \partial\Omega, \end{array} \right.$ (2.49)

$\displaystyle n\ge 2, (\tilde{\mathcal{P}}_n) \left\{ \begin{array}{lll} -di... ... sur & \sigma, \partial_n u_n = 0 & sur & \partial\Omega. \end{array} \right.$ (2.50)

On peut alors définir la fonction suivante:

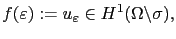$\displaystyle f(\varepsilon) := u_\varepsilon \in H^1(\Omega\backslash\sigma),$ (2.51)

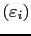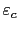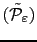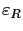qui admet le développement en série entière (2.48) autour de l'origine. On considère alors une famille de points $ (\varepsilon_i)$ choisis dans un intervalle $ [\varepsilon_c,\varepsilon_R]$ , où $ \varepsilon_c$ est une valeur critique pour laquelle on estime qu'il n'est plus raisonnable de résoudre numériquement le problème $ (\tilde{\mathcal{P}}_\varepsilon)$ , et $ \varepsilon_R$ est inférieur au rayon de convergence de la série. À l'aide de ces points, nous pouvons définir des polynômes d'interpolation de degré arbitraire:

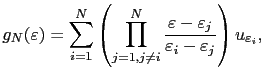$\displaystyle g_N(\varepsilon) = \sum_{i=1}^N \left( \prod_{j=1, j\ne i}^N \fra... ...arepsilon-\varepsilon_j}{\varepsilon_i-\varepsilon_j}\right) u_{\varepsilon_i},$ (2.52)

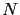où $ N$ est le nombre de points 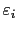$ \varepsilon_i$ choisis, et 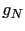$ g_N$ est alors de degré $ N-1$ .

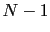L'analycité de la fonction 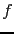$ f$ permet d'estimer l'erreur d'approximation, et d'affirmer que

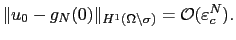$\displaystyle \Vert u_0 - g_N(0)\Vert _{H^1(\Omega\backslash\sigma)} = \mathcal{O}(\varepsilon_c^N).$ (2.53)

next up previous contents
suivant: Algorithme monter: Segmentation précédent: De la restauration à   Table des matières
Retour à la page principale