


suivant: Fast marching
monter: Couplage du gradient topologique
précédent: Couplage du gradient topologique
Table des matières
Soit 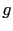 le gradient topologique, l'idée des chemins minimaux est de définir une fonction potentiel, permettant de mesurer en chaque point du domaine
le gradient topologique, l'idée des chemins minimaux est de définir une fonction potentiel, permettant de mesurer en chaque point du domaine 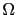 le coût pour un chemin de passer par ce point. Comme le potentiel doit être positif, nous proposons d'utiliser la fonction suivante:
le coût pour un chemin de passer par ce point. Comme le potentiel doit être positif, nous proposons d'utiliser la fonction suivante:
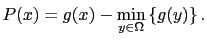 |
(2.59) |
L'avantage de ce choix est que plus le gradient topologique est négatif, plus la fonction potentielle est proche de 0
, et moins c'est coûteux pour un chemin de passer à cet endroit. À l'inverse, il est extrêmement coûteux pour un chemin de passer par un point dont le gradient topologique est positif (ou faiblement négatif).
En notant 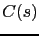 un chemin (ou une courbe) sur
un chemin (ou une courbe) sur 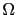 , où
, où 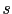 représente l'abscisse curviligne, on peut définir le coût total du chemin de la façon suivante:
représente l'abscisse curviligne, on peut définir le coût total du chemin de la façon suivante:
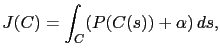 |
(2.60) |
où 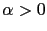 est un c
est un c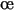 fficient de régularisation, mesurant la longueur réelle du chemin.
fficient de régularisation, mesurant la longueur réelle du chemin.
Le but est de minimiser la fonction coût 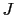 , afin par exemple de trouver le chemin le plus court (en distance) et le moins onéreux (au sens de la fonction potentiel), reliant deux points. Pour ce faire, on définit la distance suivante sur l'image:
, afin par exemple de trouver le chemin le plus court (en distance) et le moins onéreux (au sens de la fonction potentiel), reliant deux points. Pour ce faire, on définit la distance suivante sur l'image:
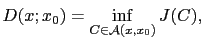 |
(2.61) |
où
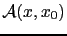 est l'ensemble des chemins reliant
est l'ensemble des chemins reliant 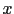 à
à 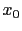 .
.



suivant: Fast marching
monter: Couplage du gradient topologique
précédent: Couplage du gradient topologique
Table des matières
Retour à la page principale
![]() le gradient topologique, l'idée des chemins minimaux est de définir une fonction potentiel, permettant de mesurer en chaque point du domaine
le gradient topologique, l'idée des chemins minimaux est de définir une fonction potentiel, permettant de mesurer en chaque point du domaine ![]() le coût pour un chemin de passer par ce point. Comme le potentiel doit être positif, nous proposons d'utiliser la fonction suivante:
le coût pour un chemin de passer par ce point. Comme le potentiel doit être positif, nous proposons d'utiliser la fonction suivante:
![]() un chemin (ou une courbe) sur
un chemin (ou une courbe) sur ![]() , où
, où ![]() représente l'abscisse curviligne, on peut définir le coût total du chemin de la façon suivante:
représente l'abscisse curviligne, on peut définir le coût total du chemin de la façon suivante:
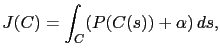
![]() , afin par exemple de trouver le chemin le plus court (en distance) et le moins onéreux (au sens de la fonction potentiel), reliant deux points. Pour ce faire, on définit la distance suivante sur l'image:
, afin par exemple de trouver le chemin le plus court (en distance) et le moins onéreux (au sens de la fonction potentiel), reliant deux points. Pour ce faire, on définit la distance suivante sur l'image: