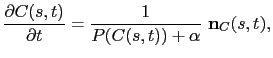 |
(2.62) |
Une façon extrêmement performante de construire la fonction distance définie par (2.61) est d'utiliser une équation de propagation d'un front:
La méthode du fast marching est la suivante: d'après la théorie des équations Eikonales, la distance ![]() est exactement l'instant
est exactement l'instant ![]() pour lequel le front
pour lequel le front ![]() initialisé en
initialisé en ![]() atteint le point
atteint le point ![]() [119,58].
[119,58].
En choisissant un point ![]() de référence, la résolution de l'équation (2.62) pour un temps suffisamment long (i.e. jusqu'à ce que tous les points aient été atteints, et donc jusqu'à ce que
de référence, la résolution de l'équation (2.62) pour un temps suffisamment long (i.e. jusqu'à ce que tous les points aient été atteints, et donc jusqu'à ce que ![]() coïncide avec le bord du domaine
coïncide avec le bord du domaine
![]() ) donne directement la distance
) donne directement la distance ![]() pour tout point
pour tout point ![]() du domaine.
du domaine.