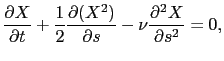Nous avons ensuite considéré un modèle non linéaire géophysique extrêmement simple, correspondant à l'équation de Burgers sur un domaine périodique en dimension 1:
 |
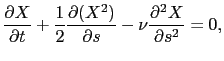(3.14) |
représente l'abscisse curviligne sur le 
parallèle nord, et 
est le temps. Ce modèle peut être vu comme la projection 1D d'un modèle bi-dimensionnel de circulation météorologique à une pression (ou altitude) fixée. Nous avons choisi la période du domaine, les intervalles de temps considérés, ainsi que la répartition spatio-temporelle des observations afin d'obtenir une situation comparable à la réalité.
Il faut noter que ce système est non linéaire, et surtout irréversible (car dissipatif) à cause du terme de diffusion. Néanmoins, nous avons constaté qu'il était possible de résoudre le problème rétrograde grâce aux observations. Les résultats numériques montrant la convergence et la comparaison de cet algorithme avec la méthode variationnelle sont détaillés dans [22]. D'autres expériences numériques dans une situation physique différente ont été réalisées dans [20].