Nous nous plaçons d'abord dans un cadre linéaire simple, qui permet de comprendre la situation. On suppose ici que l'opérateur d'observation ![]() est égal à l'identité, et que le modèle
est égal à l'identité, et que le modèle ![]() est linéaire. On suppose également que
est linéaire. On suppose également que ![]() et
et ![]() commutent, ce qui est a priori le cas dans nos applications puisqu'on choisit souvent
commutent, ce qui est a priori le cas dans nos applications puisqu'on choisit souvent ![]() proportionnel à la matrice identité. Dans ce cadre là, il est possible d'expliciter la solution de l'algorithme du nudging direct et rétrograde. Afin de simplifier considérablement les équations, on suppose ici que
proportionnel à la matrice identité. Dans ce cadre là, il est possible d'expliciter la solution de l'algorithme du nudging direct et rétrograde. Afin de simplifier considérablement les équations, on suppose ici que ![]() , mais les résultats présentés ici restent vrais dans le cas général. À l'itération
, mais les résultats présentés ici restent vrais dans le cas général. À l'itération ![]() ,
, ![]() , en supposant
, en supposant ![]() , on a
, on a
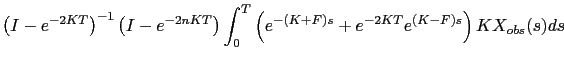 |
|||
| (3.19) |
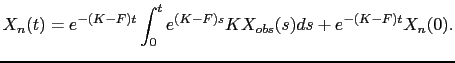 |
(3.20) |
Le résultat suivant donne alors l'existence de la trajectoire limite, et explicite sa forme [21]:
Sous les mêmes hypothèses, on peut prouver un résultat similaire pour les trajectoires rétrogrades, i.e. il existe une trajectoire limite
![]() telle que
telle que
![]() , pour tout
, pour tout
![]() . Cela prouve la convergence de l'algorithme BFN dans ce cadre là.
. Cela prouve la convergence de l'algorithme BFN dans ce cadre là.
On peut remarquer que la solution limite (en direct comme en rétrograde) ne dépend plus de la condition initiale ![]() utilisée pour initialiser l'algorithme.
utilisée pour initialiser l'algorithme.
Supposons à présent que les observations ![]() soient solutions du modèle direct (3.1). Cela implique notamment que pour tout
soient solutions du modèle direct (3.1). Cela implique notamment que pour tout
![]() ,
,
| (3.23) |
| (3.24) |
À noter que l'algorithme BFN a un comportement similaire sur les opérateurs paraboliques linéaires en dimension infinie, comme par exemple sur l'équation de la chaleur. Une décomposition des trajectoires sur une base de Fourier nous ramène à l'étude d'équations différentielles ordinaires du premier ordre sur les c![]() fficients, et donne rapidement la convergence de l'algorithme dans ce cas là.
fficients, et donne rapidement la convergence de l'algorithme dans ce cas là.