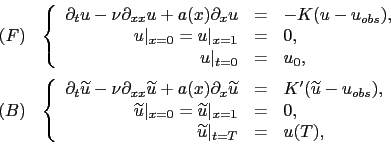Transport linéaire visqueux

suivant: Burgers visqueux monter: Équations de transport précédent: Équations de transport Table des matières

Transport linéaire visqueux

On considère tout d'abord le cas d'une équation de transport linéaire avec viscosité.

$\begin{displaymath}\begin{array}{rl} (F) & \left\{ \begin{array}{rcl} \partial_t... ...etilde{u}\vert _{t=T} &=& u(T), \end{array} \right. \end{array}\end{displaymath}$

(3.25)

avec les notations suivantes, qui restent valables dans la suite:

la période de temps considérée est $t\in[0,T]$ ;
la première équation est appelée directe (Forward), et la seconde (B) est appelée rétrograde (Backward);
et $K^\prime$ sont des fonctions scalaires positives, qui peuvent dépendre du temps et de la variable d'espace . Pour des raisons de simplicité uniquement, on suppose qu'il existe une constante $\kappa \in \mathbb{R}_{+}^*$ telle que $K^\prime(t,x) = \kappa K(t,x)$ ;
le transport $a(x)\in W^{1,\infty}(\Omega)$ , $\Omega$ étant le domaine spatial, ici soit l'intervalle , soit le tore ;
le c $\oe$ fficient de viscosité $\nu>0$ est constant;
la fonction d'observations $u_{obs}$ est solution de l'équation directe (sans nudging) avec une certaine condition initiale $u_{obs}^0$ :

$\displaystyle \left\{ \begin{array}{rcl} \partial_t u_{obs} -\nu \partial_{xx} ... ...rt _{x=0}=u\vert _{x=1}&=&0, u\vert _{t=0} &=& u_{obs}^0. \end{array} \right.$ (3.26)

Alors, nous avons le résultat suivant sur les équations de transport linéaire visqueux [30]:

Théorème 3.3 On considère une itération de l'algorithme BFN (3.25) avec des observations $u_{obs}$ vérifiant l'équation (3.26). Soient

$\begin{displaymath}\begin{array}{rcl} w(t) &=& u(t) - u_{obs}(t), \widetilde{w}(t) &=& \widetilde{u}(t)-u_{obs}(t), \end{array}\end{displaymath}$

(3.27)

les erreurs directe et rétrograde.

Si , alors pour tout $t\in[0,T]$ :

$\displaystyle \widetilde{w}(t) = e^{(-K-K^\prime)(T-t)} w(t).$ (3.28)
Si , avec $\textrm{Support }(K) \subset [a,b]$ où et $a\neq 0$ ou $b\neq 1$ , alors l'équation (3.25) est mal posée: il n'existe en général pas de solution $(u,\widetilde{u})$ .
Si $K(t,x)=K \mathbbm{1}_{[t_{1},t_{2}]}(t)$ avec $0\leq t_{1} < t_{2}\leq T$ , alors

$\displaystyle \widetilde{w}(0) = e^{(-K-K^\prime)(t_{2}-t_{1})} w(0).$ (3.29)

Ce résultat montre que dans le cas des équations de transport linéaire visqueux, l'algorithme BFN converge à condition que le terme de rappel agisse en tout point du domaine. Par exemple, dans le premier cas du théorème 3.3, l'équation (3.28) indique que l'erreur a été réduite d'un facteur $e^{(-K-K')T}$ au cours d'une itération. Par conséquent, l'erreur décroît d'un facteur $e^{-N(K+K')T}$ au cours de itérations, et la stricte positivité de (ou ) et montre la convergence de l'algorithme dans ce cas. Si par contre les observations ne sont pas disponibles partout (i.e. le support de ne recouvre pas tout le domaine), l'algorithme ne converge pas car le terme de diffusion ne peut pas être stabilisé et le problème rétrograde est alors mal posé.

suivant: Burgers visqueux monter: Équations de transport précédent: Équations de transport Table des matières

Retour à la page principale