next up previous contents
suivant: Remarques sur les résultats monter: Burgers non visqueux précédent: Burgers non visqueux   Table des matières

Remarque:

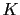Dans le cas particulier où $ K(t,x)=K(x)=K\mathbbm{1}_{[a,b]}(x)$ , où $ K$ est une constante et $ [a,b]$ est un sous-intervalle de $ [0,1]$ , alors

$\displaystyle w(T,\psi(T,x)) = w(0,x) \exp \left( - K \chi(x) -\displaystyle\int_0^T \partial_x u_{obs}(\sigma,\psi(\sigma,x))d\sigma \right),$ (3.45)

où la fonction $ \chi$ est définie par

$\displaystyle \chi(x) = \displaystyle\int_0^T \mathbbm{1}_{Supp(K)}(\psi(\sigma,x)) d\sigma$ (3.46)

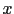et désigne le temps pendant lequel la caractéristique $ \psi(\sigma,x)$ issue de $ x$ correspondant à l'équation (3.39-F) avec 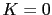$ K=0$ appartient au support de $ K$ .

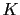On peut remarquer que le système est observable si et seulement si la fonction $ \chi$ admet une borne inférieure strictement positive, i.e. $ m := \displaystyle \min_{x} \chi(x) > 0$ , l'observabilité étant définie par (voir [94]):

% latex2html id marker 6979 $\displaystyle \exists C, \forall u \textrm{ soluti... ...avec } K=0,\quad \Vert u(T,.)\Vert^2 \le C\int_0^T \Vert K(.)u(s,.)\Vert^2\,ds.$ (3.47)

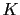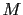Dans ce cas, la proposition 3.2 démontre la décroissance exponentielle globale (en espace) de l'erreur, du moment que $ K$ est plus grand que $ \displaystyle \frac{MT}{m}$ , où $ M$ est défini par l'équation (3.41).

Nous pouvons déduire de cette remarque que, si à chaque itération, à la fois pour la résolution du problème direct et du problème rétrograde, la condition d'observabilité est satisfaite, alors l'algorithme converge (l'erreur décroît exponentiellement vers 0 ). Il faut toutefois noter que c'est une condition suffisante mais non nécessaire, car même si $ \chi(x)=0$ , la dernière exponentielle de l'équation (3.45) est bornée.

next up previous contents
suivant: Remarques sur les résultats monter: Burgers non visqueux précédent: Burgers non visqueux   Table des matières
Retour à la page principale