


suivant: Remarque:
monter: Équations de transport
précédent: Transport linéaire non visqueux
Table des matières
On considère finalement le cas de l'équation de Burgers non visqueux, avec des conditions périodiques, pour un temps 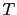 tel qu'aucun choc n'apparaisse sur l'intervalle
tel qu'aucun choc n'apparaisse sur l'intervalle ![$ [0,T]$](img343.png) :
:
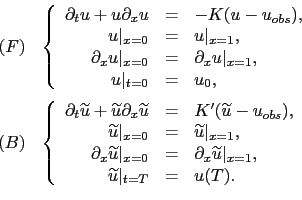 |
(3.39) |
On a alors les résultats suivants [30]:
Proposition 3.2
On considère une résolution du problème direct (resp. rétrograde) avec nudging pour l'équation de Burgers non visqueux (3.39-F) (resp. (3.39-B)). Avec les notations du théorème 3.6, si
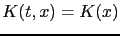 , alors
, alors
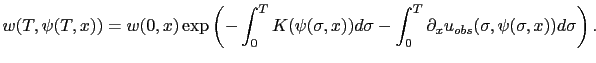 |
(3.44) |
Sous-sections



suivant: Remarque:
monter: Équations de transport
précédent: Transport linéaire non visqueux
Table des matières
Retour à la page principale
![]() tel qu'aucun choc n'apparaisse sur l'intervalle
tel qu'aucun choc n'apparaisse sur l'intervalle ![]() :
: