


suivant: Approche multi-grille et optimisation
monter: Modélisation et résolution du
précédent: Fonction coût
Table des matières
Nous avons étudié différentes régularisations, soit classiques (comme par exemple la norme 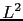 ), soit liées à la physique du problème (norme de la divergence):
), soit liées à la physique du problème (norme de la divergence):
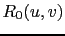 |
 |
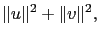 |
(4.4) |
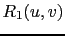 |
 |
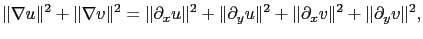 |
(4.5) |
 |
 |
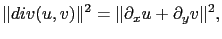 |
(4.6) |
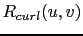 |
 |
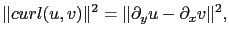 |
(4.7) |
 |
 |
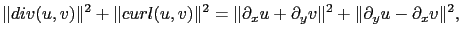 |
(4.8) |
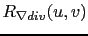 |
 |
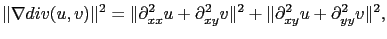 |
(4.9) |
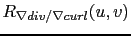 |
 |
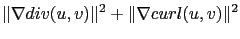 |
(4.10) |
| |
 |
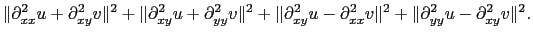 |
|
Dans la suite, on notera
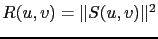 où
où 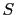 est un opérateur linéaire. Des c
est un opérateur linéaire. Des c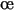 fficients peuvent être introduits pour pondérer les différents termes entre eux.
fficients peuvent être introduits pour pondérer les différents termes entre eux.



suivant: Approche multi-grille et optimisation
monter: Modélisation et résolution du
précédent: Fonction coût
Table des matières
Retour à la page principale
![]() ), soit liées à la physique du problème (norme de la divergence):
), soit liées à la physique du problème (norme de la divergence):