Dans cette partie, nous supposons que le domaine ![]() contient une fissure
contient une fissure
![]() . On impose un flux
. On impose un flux
![]() sur le bord
sur le bord ![]() du domaine
du domaine ![]() , et on veut trouver
, et on veut trouver
![]() telle que la solution
telle que la solution
![]() de
de
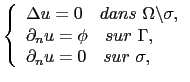 |
(2.7) |
Une approche par gradient topologique a été introduite dans [9], et consiste à définir deux solutions différentes à partir des deux données de Dirichlet et Neumann:
En remarquant que les deux solutions coïncident si
![]() , l'idée consiste à minimiser la fonction coût
, l'idée consiste à minimiser la fonction coût
Le développement asymptotique topologique de cette fonctionnelle est détaillé dans [9].