Dans notre approche, ![]() représente désormais l'image, on note
représente désormais l'image, on note ![]() sa frontière, et on dénote par
sa frontière, et on dénote par
![]() la partie cachée (inconnue) de l'image, et
la partie cachée (inconnue) de l'image, et ![]() sa frontière. Soit
sa frontière. Soit ![]() l'image dégradée et que l'on souhaite reconstituer. On suppose donc que
l'image dégradée et que l'on souhaite reconstituer. On suppose donc que ![]() est connue sur
est connue sur
![]() , et inconnue sur
, et inconnue sur ![]() .
.
L'idée consiste à adapter la méthode de localisation des fissures à l'inpainting: nous allons chercher à identifier les fissures, ou contours, ![]() dans la partie cachée
dans la partie cachée ![]() de l'image, puis imposer que le Laplacien de l'image reconstruite soit nul dans
de l'image, puis imposer que le Laplacien de l'image reconstruite soit nul dans
![]() . Pour une fissure
. Pour une fissure ![]() donnée (i.e. pour un contour donné dans la partie cachée de l'image), et en utilisant la connaissance de
donnée (i.e. pour un contour donné dans la partie cachée de l'image), et en utilisant la connaissance de ![]() (donnée de Dirichlet) et de son flux (donnée de Neumann) sur le bord
(donnée de Dirichlet) et de son flux (donnée de Neumann) sur le bord ![]() de
de ![]() , on peut reconstruire deux solutions différentes à l'intérieur de
, on peut reconstruire deux solutions différentes à l'intérieur de ![]() .
.
Pour une fissure ![]() donnée dans
donnée dans ![]() , la solution
, la solution
![]() du problème de Dirichlet vérifie
du problème de Dirichlet vérifie
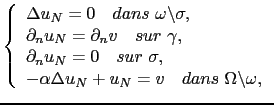 |
(2.13) |