Algorithme dual pour le modèle quasi-géostrophique

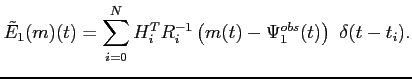
suivant: Résultats numériques monter: Algorithme dual précédent: Lien avec la méthode Table des matières

Algorithme dual pour le modèle quasi-géostrophique

Voyons maintenant comment l'algorithme dual peut être utilisé dans le cas d'un modèle non linéaire, le modèle quasi-géostrophique barocline. Nous rappelons qu'un des avantages de la méthode duale est qu'elle couvre aussi la méthode primale dans un cadre linéaire. En effet, la méthode duale agit sur les matrices de covariance d'erreur directes et en faisant tendre la matrice de covariance d'erreur modèle vers zéro, la méthode n'est pas perturbée et devient équivalente à la méthode primale pour un problème sans erreur modèle.

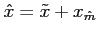
Du fait de la non linéarité du modèle, la trajectoire utilisée pour linéariser le modèle autour d'un état de référence évolue ici à chaque itération, et nous avons donc abandonné l'écriture sous forme incrémentale $\hat{x}=\tilde{x}+x_{\hat{m}}$ . Nous devons donc construire un nouvel algorithme dual pour notre modèle qui consiste à calculer une fonction coût duale de la fonctionnelle primale (comme indiqué dans le paragraphe 2.2 du chapitre 2) via une linéarisation adéquate autour d'un état de référence. 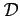La difficulté majeure de l'algorithme dual vient du fait que la trajectoire utilisée pour linéariser le modèle est réactualisée à chaque itération, et par conséquent, les opérateurs d'observation linéarisés et $\mathcal{D}$ aussi. La fonction coût duale change donc aussi à chaque itération dans le processus de minimisation.

L'algorithme dans le cas non linéaire se présente sous la forme suivante :

Soit un vecteur d'observations qui peut être relié directement à $\Psi_1$ (supposons par exemple que contient les observations d'une partie de la surface de l'océan à différents instants ). Donnons nous un état de référence du modèle (une ébauche) afin de pouvoir linéariser le modèle et les opérateurs d'observation.
On résout les équations adjointes, provenant d'une linéarisation du modèle autour de la trajectoire issue de l'ébauche :

$\begin{displaymath}\begin{array}{rcl} \displaystyle \frac{\partial \theta_1^T(\L... ...alpha\Delta\Lambda_n-\beta\Delta^2\Lambda_n = 0, \end{array}\end{displaymath}$ (5.35)

avec les conditions finales $\Lambda_k(T)=0$ , $1\le k\le n$ , et

$\displaystyle \tilde{E}_1(m)(t)=\sum_{i=0}^NH_i^TR_i^{-1}\left( m(t)-\Psi_1^{obs}(t) \right) \delta(t-t_i).$
Il faut ensuite résoudre les équations directes non linéaires :

$\begin{displaymath}\begin{array}{l} \displaystyle \frac{D_1\left( \theta_1(\Psi)... ...\Delta\Psi_n -\beta\Delta^2\Psi_n =(Q\Lambda)_n, \end{array}\end{displaymath}$ (5.36)

avec les conditions initiales

$\displaystyle \Psi_k(0)=\Psi_k^e(0)+\left( P_0\Lambda(0) \right)_k,$ (5.37)

où et sont des matrices de préconditionnement statistique et $\Psi_k^e(0)$ est une estimation a priori de l'état initial $\Psi_k(0)$ .
La trajectoire obtenue servira de nouvelle ébauche du système pour la prochaine itération.
On définit alors l'opérateur $\mathcal{D}$ (dépendant de l'état autour duquel a été linéarisé le problème) agissant sur l'espace des observations :

$\displaystyle (\mathcal{D}m)(t)=\sum_{i=0}^N H_i\Psi_1(t_i) \delta(t-t_i),$ (5.38)

les opérateurs d'observation ayant été linéarisés avec le modèle.

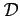
Une fois l'opérateur $\mathcal{D}$ construit, il ne reste plus qu'à utiliser la théorie vue précédemment pour définir la fonction coût duale :

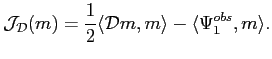$\displaystyle \mathcal{J}_\mathcal{D}(m)=\frac{1}{2} \langle \mathcal{D}m,m\rangle - \langle \Psi_1^{obs},m\rangle.$

(5.39)

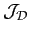
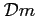
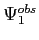
La fonctionnelle $\mathcal{J}_\mathcal{D}$ mesure l'écart entre $\mathcal{D}m$ et $\Psi_1^{obs}$ , c'est-à-dire entre la trace dans l'espace des observations de la solution du modèle direct et le vecteur des observations du système.

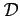
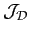
Comme l'opérateur $\mathcal{D}$ est linéaire symétrique défini positif, la gradient de $\mathcal{J}_\mathcal{D}$ est immédiat :

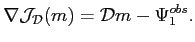$\displaystyle \nabla \mathcal{J}_\mathcal{D}(m) = \mathcal{D}m - \Psi_1^{obs}.$

(5.40)

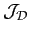
Nous avons maintenant tout ce qu'il faut pour appliquer un algorithme de minimisation de la fonction coût duale $\mathcal{J}_\mathcal{D}$ , en utilisant simplement une méthode itérative de type quasi-Newton comme par exemple un algorithme L-BFGS, et en réactualisant à chaque itération la fonction coût duale avec la nouvelle ébauche obtenue.

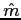
En supposant le minimum $\hat{m}$ identifié, il est alors facile de reconstruire la trajectoire correspondante dans l'espace des états : il suffit de résoudre les équations (5.35) et (5.36), la condition initiale dans l'espace des états étant donné par la formule (5.37).

On observe à nouveau que la fonctionnelle duale est définie sur un espace (celui des observations) de dimension plus petite que la fonctionnelle primale (définie sur l'espace des états). La minimisation de la fonctionnelle duale ne coûte donc pas plus cher que la minimisation de la fonctionnelle primale. De plus, cet algorithme tient toujours compte de l'erreur modèle, ce qui était numériquement impossible avec l'approche primale du 4D-VAR.

suivant: Résultats numériques monter: Algorithme dual précédent: Lien avec la méthode Table des matières

Retour à la page principale