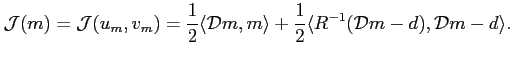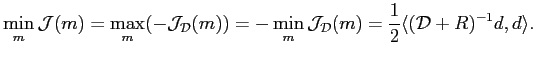Lien avec la méthode primale

Nous avons le théorème suivant qui permet de relier les deux approches et de montrer qu'elles sont équivalentes :

Théorème 5.1 En posant et , on peut redéfinir la fonctionnelle primale $\mathcal{J}$ comme étant une fonction de uniquement :

$\displaystyle \mathcal{J}(m)=\mathcal{J}(u_m,v_m)=\frac{1}{2}\langle \mathcal{D}m,m\rangle + \frac{1}{2} \langle R^{-1}(\mathcal{D}m-d),\mathcal{D}m-d\rangle.$

(5.33)

On a alors

$\displaystyle \min_{m}\mathcal{J}(m) = \max_{m}(-\mathcal{J}_\mathcal{D}(m)) = ... ...\mathcal{J}_\mathcal{D}(m) =\frac{1}{2} \langle (\mathcal{D}+R)^{-1}d,d\rangle.$

(5.34)

De plus, les minima sont réalisés au même point .

$\blacksquare$

Démonstration : Commençons par expliciter le second membre de (5.33) :

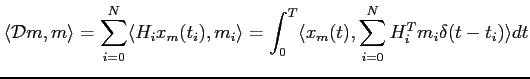
$\displaystyle \langle \mathcal{D}m,m \rangle=\sum_{i=0}^N \langle H_ix_m(t_i),m_i \rangle =\int_0^T\langle x_m(t),\sum_{i=0}^N H_i^T m_i \delta(t-t_i)\rangle dt$

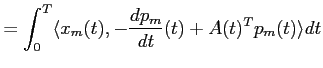
$\displaystyle =\int_0^T \langle x_m(t), -\frac{dp_m}{dt}(t)+A(t)^Tp_m(t)\rangle dt$

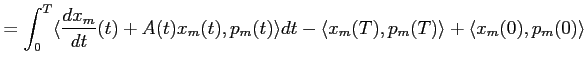
$\displaystyle =\int_0^T \langle \frac{dx_m}{dt}(t)+A(t)x_m(t), p_m(t)\rangle dt -\langle x_m(T),p_m(T)\rangle + \langle x_m(0),p_m(0)\rangle$

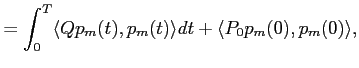
$\displaystyle =\int_0^T \langle Qp_m(t),p_m(t)\rangle dt + \langle P_0p_m(0), p_m(0)\rangle,$

et on retrouve les deux derniers termes de $\mathcal{J}$ dans la formule (5.22), compte tenu du fait que

De plus, $\mathcal{D}m-d=Hx_m-(y-H\tilde{x})=H(\tilde{x}+x_m)-z$ et $\tilde{x}+x_m$ est solution de l'équation (5.21) avec et . On retombe donc bien sur le premier terme de $\mathcal{J}(u_m,v_m)$ .

Dérivons maintenant $\mathcal{J}(m)$ :

$\displaystyle \nabla\mathcal{J}(m)=\mathcal{D}m+\mathcal{D}R^{-1}(\mathcal{D}m-d)$

donc au minimum $m^\ast$ de $\mathcal{J}$ , on a

$\displaystyle \nabla\mathcal{J}(m^\ast)=0 \textrm{ (i.e.) } m^\ast+R^{-1}(\mathcal{D}m^\ast -d)=0 \textrm{ (i.e.) } R^{-1}(R+\mathcal{D})m^\ast = R^{-1}d,$

d'où on tire que

$\displaystyle \min_m \mathcal{J}(m)=\mathcal{J}(m^\ast) \textrm{ avec } m^\ast=(\mathcal{D}+R)^{-1}d=\hat{m},$

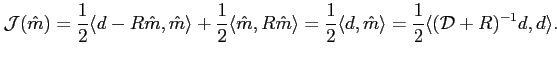
$\displaystyle \mathcal{J}(\hat{m})=\frac{1}{2}\langle d-R\hat{m},\hat{m}\rangle... ...\langle d,\hat{m} \rangle = \frac{1}{2} \langle (\mathcal{D}+R)^{-1}d,d\rangle.$

Par construction de $\mathcal{J}_\mathcal{D}$ , on a clairement

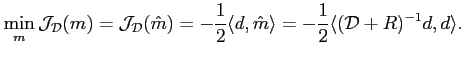
$\displaystyle \min_m \mathcal{J}_\mathcal{D}(m) =\mathcal{J}_\mathcal{D}(\hat{... ...2}\langle d,\hat{m}\rangle =-\frac{1}{2}\langle (\mathcal{D}+R)^{-1}d,d\rangle.$

$\quad \square$

Le théorème 5.1 démontre l'équivalence des deux approches en terme de construction des solutions, ainsi que l'égalité des solutions construites et des extréma des fonctionnelles. Il y a cependant deux avantages nets en faveur de la méthode duale :

la prise en compte inhérente de l'erreur modèle,
et la minimisation de la fonction coût duale se fait dans l'espace des observations, de dimension inférieure à l'espace des états pour la fonctionnelle primale.

suivant: Algorithme dual pour le monter: Description théorique précédent: Approche duale Table des matières

Retour à la page principale